Xét chiều biến thiên và vẽ đồ thị của các hàm số:

$a) y=\frac{1}{2}x-1;$

$$\begin{gathered} b) y=4-2x; \\ c) y=\sqrt{x^2}; \\ d) y=\left|x+1\right|. \end{gathered}$$

a) Hàm số  có:

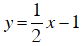
+ Tập xác định D = R.

+ Có 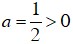 nên hàm số đồng biến trên R.

+ Tại x = 0 thì y = 1/2 . 0 – 1 = –1 . Vậy A (0; –1) thuộc đồ thị hàm số.

Tại x = 2 thì y = 1/2 . 2 – 1 = 0. Vậy B (2; 0) thuộc đồ thị hàm số.

Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A (0; –1) và B (2; 0).

b) Hàm số y = 4 – 2x có:

+ Tập xác định D = R

+ Có a = –2 < 0 nên hàm số nghịch biến trên R.

+ Tại x = 0 thì y = 4 ⇒ A(0 ; 4) thuộc đồ thị hàm số.

Tại x = 2 thì y = 0 ⇒ B(2; 0) thuộc đồ thị hàm số.

Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A(0 ; 4) và B(2; 0).

c)

+ Tập xác định: R

+ Trên (–1; +∞), y = x + 1 hàm số đồng biến.

Trên (-∞; -1), y = - x - 1 hàm số nghịch biến.

Bảng biến thiên :

+ Đồ thị hàm số gồm hai phần:

Phần thứ nhất: Nửa đường thẳng y = –x giữ lại phần bên trái trục tung.

Phần thứ hai: Nửa đường thẳng y = x giữ lại phần bên phải trục tung.

d) Hàm số y = |x + 1|

Nếu x + 1 ≥ 0 hay x ≥ –1 thì y = x + 1.

Nếu x + 1 < 0 hay x < –1 thì y = –(x + 1) = –x – 1. 

+ Tập xác định: R

+ Trên (–∞; –1), y = x + 1 đồng biến.

Trên (–1 ; +∞), y = –x – 1 nghịch biến.

Ta có bảng biến thiên :

+ Đồ thị hàm số gồm hai phần:

Phần thứ nhất : Nửa đường thẳng y = x + 1 giữ lại các điểm có hoành độ ≥ –1.

Phần thứ hai : nửa đường thẳng y = –x – 1 giữ lại các điểm có hoành độ < –1.

Kiến thức áp dụng

+ Hàm số y = ax + b đồng biến trên tập xác định nếu a > 0 và nghịch biến trên tập xác định nếu a < 0.

+ Đồ thị hàm số y = ax + b là đường thẳng nên ta chỉ cần xác định hai điểm thuộc đồ thị rồi vẽ đường thẳng qua nó.