Giải SBT Toán 7 Bài tập cuối chương 5 có đáp án
-
52 lượt thi
-
24 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Biểu đồ cột kép ở Hình 21 biểu diễn kết quả điểm trung bình Học kì II của các môn: Ngữ văn, Toán, Tiếng Anh, Giáo dục công dân, Lịch sử và Địa lí, Khoa học tự nhiên, Công nghệ, Tin học, của hai học sinh Lan và Hà ở một trường trung học cơ sở.
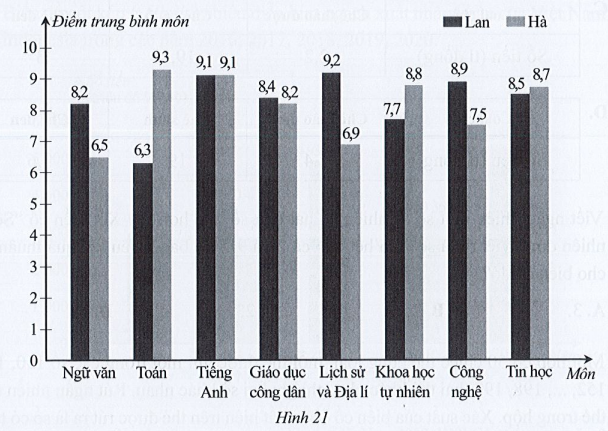
Chênh lệch tổng số điểm trung bình Học kì II các môn trên của hai học sinh Lan và Hà là:
A. 1,5 điểm;
B. 1,1 điểm;
C. 0,8 điểm;
D. 1,3 điểm.
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
‒ Nhìn vào cột (màu đậm) của biểu đồ cột kép ở Hình 21 biểu thị kết quả điểm trung bình Học kì II môn Ngữ văn của bạn Lan, ta thấy trên đỉnh cột đó ghi số 8,2 và đơn vị tính ghi trên trục thẳng đứng là điểm trung bình môn. Vậy điểm trung bình môn Ngữ Văn của bạn Lan là 8,2.
Tương tự như trên, ta xác định được điểm trung bình môn Toán, Tiếng Anh, Giáo dục công dân, Lịch sử và Địa lí, Khoa học tự nhiên, Công nghệ, Tin học của bạn Lan lần lượt là: 6,3; 9,1; 8,4; 9,2; 7,7; 8,9; 8,5.
Do đó, tổng điểm trung bình Học kì II các môn của bạn Lan là:
8,2 + 6,3 + 9,1 + 8,4 + 9,2 + 7,7 + 8,9 + 8,5 = 66,3.
‒ Nhìn vào cột (màu nhạt) của biểu đồ cột kép ở Hình 21 biểu thị kết quả điểm trung bình Học kì II môn Ngữ văn của bạn Hà, ta thấy trên đỉnh cột đó ghi số 6,5 và đơn vị tính ghi trên trục thẳng đứng là điểm trung bình môn. Vậy điểm trung bình môn Ngữ Văn của bạn Hà là 6,5.
Tương tự như trên, ta xác định được điểm trung bình môn Toán, Tiếng Anh, Giáo dục công dân, Lịch sử và Địa lí, Khoa học tự nhiên, Công nghệ, Tin học của bạn Hà lần lượt là: 9,3; 9,1; 8,2; 6,9; 8,8; 7,5; 8,7.
Do đó, tổng điểm trung bình Học kì II các môn của bạn Hà là:
6,5 + 9,3 + 9,1 + 8,2 + 6,9 + 8,8 + 7,5 + 8,7 = 65.
Chênh lệch tổng số điểm trung bình Học kì II các môn trên của Lan và Hà là:
66,3 – 65 = 1,3.
Vậy ta chọn phương án D.
Câu 2:
Trong năm 2020, công ty chè Phú Minh thu được 25 tỉ đồng từ việc xuất khẩu chè. Biểu đồ hình quạt tròn ở Hình 22 biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các loại chè xuất khẩu trong năm 2020 của công ty Phú Minh.
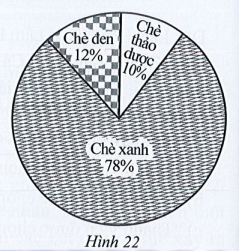
Bảng nào sau đây là bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè năm 2020?
A.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,1 |
3,2 |
B.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
C.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,2 |
19,2 |
3 |
D.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,4 |
19 |
3,6 |
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
Dựa vào biểu đồ biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các loại chè xuất khẩu trong năm 2020 của công ty Phú Minh ta có tỉ số phần trăm các loại là:
• Chè thảo dược: 10%;
• Chè xanh: 78%.
• Chè đen: 12%;
Khi đó, ta có:
• Số tiền công ty chè Phú Minh thu được ở chè thảo dược năm 2020 là:
25 . 10% = 25 . \(\frac{{10}}{{100}}\) = 2,5 (tỉ đồng).
• Số tiền công ty chè Phú Minh thu được ở chè xanh năm 2020 là:
25 . 78% = 25 . \(\frac{{78}}{{100}}\) = 19,5 (tỉ đồng).
• Số tiền công ty chè Phú Minh thu được ở chè đen năm 2020 là:
25 . 12% = 25 . \(\frac{{12}}{{100}}\) = 3 (tỉ đồng).
Vậy ta có bảng số liệu sau:
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
Vậy ta chọn phương án B.
Câu 3:
Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 70. Xét biến cố “Số tự nhiên được viết ra là số chia hết cho cả 2 và 9”. Có bao nhiêu kết quả thuận lợi cho biến cố đó?
A. 3;
B. 2;
C. 23;
D. 22.
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Tập hợp các kết quả có thể xảy ra đối với số tự nhiên có hai chữ số nhỏ hơn 70 được viết ra là: M = {10, 11, 12,..., 68, 69}.
Trong các số 10, 11, 12,..., 68, 69, có 3 số là số chia hết cho cả 2 và 9 là: 18, 36, 54.
Vậy có 3 kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số chia hết cho cả 2 và 9” là: 18, 36, 54 (lấy ra từ tập hợp M = {10, 11, 12,..., 68, 69}).
Vậy ta chọn phương án A.
Câu 4:
Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 150, 151, 152, …, 198, 199; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số có tổng ba chữ số bằng 12” là:
A. \(\frac{2}{{25}}\);
B. \(\frac{7}{{50}}\);
C. \(\frac{4}{{25}}\);
D. \(\frac{1}{{10}}\).
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:
M = {150, 151, 152,..., 198, 199}.
Số các phần tử của tập hợp M là 199 – 150 + 1 = 50.
Trong các số 150, 151, 152,..., 198, 199, có 5 số có tổng ba chữ số bằng 12 là: 156, 165, 174, 183, 192.
Vậy có 5 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có tổng ba chữ số bằng 12” là: 156, 165, 174, 183, 192 (lấy ra từ tập hợp M = {150, 151, 152,..., 198, 199}).
Do đó, xác xuất của biến cố “Số xuất hiện trên thẻ được rút ra là số có tổng ba chữ số bằng 12” là: \(\frac{5}{{50}} = \frac{1}{{10}}\).
Vậy ta chọn phương án D.
Câu 5:
Bốn học sinh An, Bình, Minh, Hằng đã sắp xếp thời gian luyện tập cho giải Bóng rổ năng khiếu. Biểu đồ ở Hình 23 biểu diễn thời gian luyện tập trong ngày của bốn bạn đó.
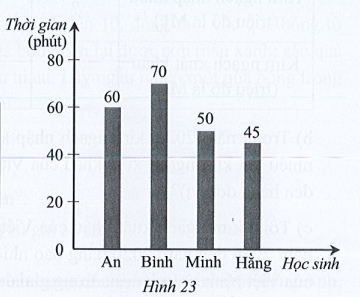
Lập bảng số liệu thống kê thời gian luyện tập của bốn học sinh trên theo mẫu sau:
|
Học sinh |
An |
Bình |
Minh |
Hằng |
|
Thời gian (phút) |
? |
? |
? |
? |
 Xem đáp án
Xem đáp án
Lời giải
Nhìn vào biểu đồ Hình 23 biểu diễn thời gian luyện tập trong ngày của bốn bạn An, Bình, Minh, Hằng, ta thấy trên đỉnh cột tương ứng ghi số 60, 70, 50, 45 và đơn vị tính ghi trên trục thẳng đứng là thời gian (phút). Từ đó ta có bảng số liệu thống kê thời gian luyện tập của bốn học sinh như sau:
|
Học sinh |
An |
Bình |
Minh |
Hằng |
|
Thời gian (phút) |
60 |
70 |
50 |
45 |
Câu 6:
 Xem đáp án
Xem đáp án
Lời giải
Thời gian luyện tập của bạn Bình là: 70 phút.
Tổng thời gian luyện tập của ba bạn An, Minh, Hằng là: 60 + 50 + 45 = 155 (phút).
Tỉ số giữa tổng số giữa thời gian luyện tập của bạn Bình với tổng thời gian luyện tập của ba bạn An, Minh, Hằng là: \(\frac{{70}}{{155}} = \frac{{14}}{{31}}\).
Vậy tỉ số giữa thời gian luyện tập của bạn Bình với tổng thời gian luyện tập của ba bạn An, Minh, Hằng bằng \(\frac{{14}}{{31}}.\)
Câu 7:
 Xem đáp án
Xem đáp án
Lời giải
Thời gian luyện tập của bạn Hằng là: 45 phút;
Thời gian luyện tập của bạn An là: 60 phút.
Tỉ số phần trăm thời gian luyện tập của bạn Hằng so với thời gian luyện tập của bạn An là:
\(\frac{{45}}{{60}}\) . 100% = 75%.
Vậy thời gian luyện tập của bạn Hằng bằng 75% thời gian luyện tập của bạn An.
Câu 8:
Biểu đồ cột kép ở Hình 24 biểu diễn kim ngạch xuất nhập khẩu của Việt Nam với Indonesia trong các năm 2016, 2017, 2018, 2019, 2020.
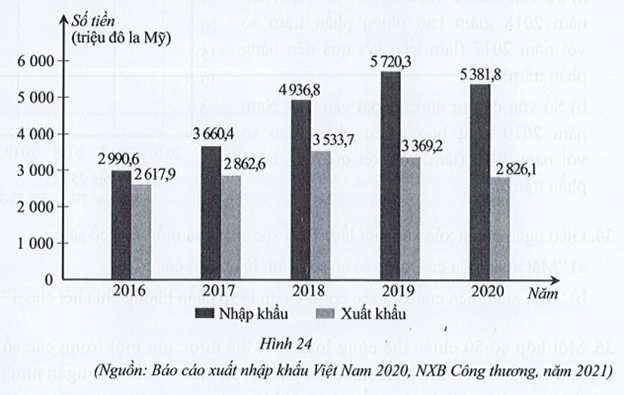
Lập bảng số liệu thống kê kim ngạch xuất nhập khẩu của Việt Nam với Indonesia theo mẫu sau:
|
Năm |
2016 |
2017 |
2018 |
2019 |
2020 |
|
Kim ngạch nhập khẩu (triệu đô la Mỹ) |
? |
? |
? |
? |
? |
|
Kim ngạch xuất khẩu (triệu đô la Mỹ) |
? |
? |
? |
? |
? |
 Xem đáp án
Xem đáp án
Lời giải
‒ Nhìn vào cột (màu đậm) của biểu đồ cột kép ở Hình 24 biểu thị kim ngạch nhập khẩu của Việt Nam từ Indonesia trong năm 2016, ta thấy trên đỉnh cột đó ghi số 2 990,6 và đơn vị tính ghi trên trục thẳng đứng là triệu đô la Mỹ. Vậy kim ngạch nhập khẩu của Việt Nam từ Indonesia trong năm 2016 là 2 990,6 triệu đô la Mỹ.
Tương tự như trên, ta xác định được kim ngạch nhập khẩu của Việt Nam từ Indonesia trong các năm 2017, 2018, 2019, 2020 lần lượt là: 3 660,4; 4 936,8; 5 720,3; 5 381,8 (triệu đô la Mỹ).
‒ Nhìn vào cột (màu nhạt) của biểu đồ cột kép ở Hình 24 biểu thị kim ngạch xuất khẩu của Việt Nam sang Indonesia trong năm 2016, ta thấy trên đỉnh cột đó ghi số 2 617,9 và đơn vị tính ghi trên trục thẳng đứng là triệu đô la Mỹ. Vậy kim ngạch xuất khẩu của Việt Nam sang Indonesia trong năm 2016 là 2 617,9 triệu đô la Mỹ.
Tương tự như trên, ta xác định được kim ngạch nhập khẩu của Việt Nam sang Indonesia trong các năm 2017, 2018, 2019, 2020 lần lượt là: 2 862,6; 3 533,7; 3 369,2; 2 826,1 (triệu đô la Mỹ).
Ta có bảng số liệu sau:
|
Năm |
2016 |
2017 |
2018 |
2019 |
2020 |
|
Kim ngạch nhập khẩu (triệu đô la Mỹ) |
2 990,6 |
3 660,4 |
4 936,8 |
5 720,3 |
5 381,8 |
|
Kim ngạch xuất khẩu (triệu đô la Mỹ) |
2 617,9 |
2 862,6 |
3 533,7 |
3 369,2 |
2 826,1 |
Câu 9:
 Xem đáp án
Xem đáp án
Lời giải
Trong năm 2020, kim ngạch nhập khẩu của Việt Nam từ Indonesia gấp số lần kim ngạch xuất khẩu của Việt Nam sang Indonesia là: \(\frac{{5\,\,381,8}}{{2\,\,826,1}}\) ≈ 2 (lần).
Vậy trong năm 2020, kim ngạch nhập khẩu của Việt Nam từ Indonesia gấp khoảng 2 lần kim ngạch xuất khẩu của Việt Nam sang Indonesia.
Câu 10:
 Xem đáp án
Xem đáp án
Lời giải
Tổng kim ngạch nhập khẩu của Việt Nam từ Indonesia trong giai đoạn từ năm 2016 đến năm 2020 là:
2 990,6 + 3 660,4 + 4 936,8 + 5 720,3 + 5 381,8 = 22 689,9 (triệu đô la Mỹ).
Tổng kim ngạch xuất khẩu của Việt Nam sang Indonesia trong giai đoạn từ năm 2016 đến năm 2020 là:
2 617,9 + 2 862,6 + 3 533,7 + 3 369,2 + 2 826,1 = 15 209,5 (triệu đô la Mỹ).
Vậy tỉ số phần trăm tổng kim ngạch xuất khẩu của Việt Nam sang Indonesia trong giai đoạn từ năm 2016 đến năm 2020 và tổng kim ngạch nhập khẩu của Việt Nam từ Indonesia trong giai đoạn từ năm 2016 đến năm 2020 là:
\(\frac{{15\,\,209,5}}{{22\,\,689,9}}\) . 100% ≈ 67%.
Vậy tổng kim ngạch xuất khẩu của Việt Nam sang Indonesia trong giai đoạn từ năm 2016 đến năm 2020 bằng khoảng 67% tổng kim ngạch nhập khẩu của Việt Nam từ Indonesia trong giai đoạn từ năm 2016 đến năm 2020.
Câu 11:
Biểu đồ đoạn thẳng ở Hình 25 biểu diễn số vốn đầu tư nước ngoài vào Việt Nam trong các năm 2016, 2017, 2018, 2019.
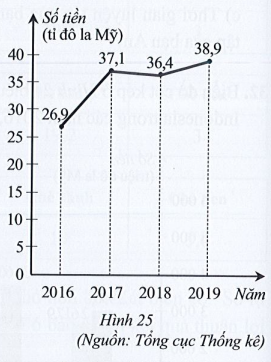
Số vốn đầu tư nước ngoài vào Việt Nam năm 2018 giảm bao nhiêu phần trăm so với năm 2017 (làm tròn kết quả đến hàng phần trăm)?
 Xem đáp án
Xem đáp án
Lời giải
Dựa vào biểu đồ Hình 25 ta có:
Số vốn đầu tư nước ngoài vào Việt Nam năm 2017 là: 37,1 tỉ đô la Mỹ;
Số vốn đầu tư nước ngoài vào Việt Nam năm 2018 là: 36,4 tỉ đô la Mỹ.
Do đó, tỉ số phần trăm số vốn đầu tư nước ngoài vào Việt Nam năm 2018 so với năm 2017 là: \(\frac{{36,4}}{{37,1}}\) . 100% ≈ 98,11%.
Vậy số vốn đầu tư nước ngoài vào Việt Nam năm 2018 giảm 100% ‒ 98,11% = 1,89% so với năm 2017.
Câu 12:
 Xem đáp án
Xem đáp án
Lời giải
Dựa vào biểu đồ Hình 25 ta có:
Số vốn đầu tư nước ngoài vào Việt Nam năm 2016 là: 26,9 tỉ đô la Mỹ;
Số vốn đầu tư nước ngoài vào Việt Nam năm 2019 là: 38,9 tỉ đô la Mỹ.
Do đó, tỉ số phần trăm số vốn đầu tư nước ngoài vào Việt Nam năm 2019 so với năm 2016 là: \(\frac{{38,9}}{{26,9}}\) . 100% ≈ 144,61%.
Vậy số vốn đầu tư nước ngoài vào Việt Nam năm 2019 tăng 144,61% - 100% = 44,61% so với năm 2016.
Câu 13:
Gieo ngẫu nhiêu xúc xắc một lần. Tính xác suất của mỗi biến cố sau:
“Mặt xuất hiện của xúc xắc có số chấm là ước số của 5”;
 Xem đáp án
Xem đáp án
Lời giải
Tập hợp các kết quả có thể xảy ra đối với xúc xắc là:
A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.
Trong các số 1, 2, 3, 4, 5, 6, có hai số là ước của 5 là: 1, 5.
Vậy có 2 kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước số của 5” là: mặt 1 chấm, mặt 5 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).
Xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước số của 5” là: \(\frac{2}{6} = \frac{1}{3}.\)
Câu 14:
 Xem đáp án
Xem đáp án
Lời giải
Trong các số 1, 2, 3, 4, 5, 6, có hai số là số chẵn không chia hết cho 4 là: 2, 6.
Vậy có 2 kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn không chia hết cho 4” là: mặt 2 chấm, mặt 6 chấm (lấy ra từ tập hợp A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}).
Xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn không chia hết cho 4” là: \(\frac{2}{6} = \frac{1}{3}.\)
Câu 15:
Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 49, 50; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
“Số xuất hiện trên thẻ được rút ra là số lớn hơn 25”;
 Xem đáp án
Xem đáp án
Lời giải
Tập hợp C gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:
C = {1, 2, 3, …, 49, 50}.
Số các phần tử của tập hợp C là 50.
Trong các số 1, 2, 3, ..., 49, 50, có 25 số có hai chữ số lớn hơn 25 là: 26, 27, 28, ..., 49, 50.
Vậy có 25 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra lớn hơn 25” là: 26, 27, 28,...,49, 50 (lấy ra từ tập hợp C = {1, 2, 3, …, 49, 50}).
Do đó, xác xuất của biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ số lớn hơn 25” là: \(\frac{{25}}{{50}} = \frac{1}{2}\).
Câu 16:
 Xem đáp án
Xem đáp án
Lời giải
Trong các số 1, 2, 3, ..., 49, 50, có 14 số có chứa chữ số 3 là là: 3, 13, 23, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 43.
Vậy có 14 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 3” là: 3, 13, 23, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 43 (lấy ra từ tập hợp C = {1, 2, 3, …, 49, 50}).
Do đó, xác xuất của biến cố “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 3” là: \(\frac{{14}}{{50}} = \frac{7}{{25}}\).
Câu 17:
 Xem đáp án
Xem đáp án
Lời giải
Trong các số 1, 2, 3, ..., 49, 50, có một số chia cho 11 dư 2 và chia cho 5 dư 3 là: 13.
Vậy có một kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số khi chia cho 11 dư 2 và chia cho 5 dư 3” là: 13 (lấy ra từ tập hợp C = {1, 2, 3, …, 49, 50}).
Do đó, xác xuất của biến cố “Số xuất hiện trên thẻ được rút ra là số khi chia cho 11 dư 2 và chia cho 5 dư 3” là: \(\frac{1}{{50}}\).
Câu 18:
Một hộp có 10 quả bóng đánh số từ 1 đến 10, đồng thời các quả bóng từ 1 đến 6 được sơn màu vàng và các quả bóng còn lại được sơn màu xanh; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp. Tính xác suất của mỗi biến cố sau:
“Quả bóng được chọn ra màu vàng”;
 Xem đáp án
Xem đáp án
Lời giải
Do các quả bóng có kích thước và khối lượng như nhau nên khả năng được chọn là như nhau nên tập hợp các kết quả có thể xảy ra đối với quả bóng được chọn ra là:
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Trong số các quả bóng được chọn, có 6 quả có màu vàng được đánh số là: 1, 2, 3, 4, 5, 6.
Vậy có 6 kết quả thuận lợi cho biến cố “Quả bóng được chọn ra màu vàng” là: 1, 2, 3, 4, 5, 6 (lấy ra từ tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}).
Do đó, xác xuất của biến cố “Quả bóng được chọn ra màu vàng” là: \(\frac{6}{{10}} = \frac{3}{5}\).
Câu 19:
 Xem đáp án
Xem đáp án
Lời giải
Do có tất cả 10 quả bóng, 6 quả bóng màu vàng đánh số: 1, 2, 3, 4, 5, 6 nên còn lại có 4 quả màu xanh đánh số: 7, 8, 9, 10.
Vậy có 4 kết quả thuận lợi cho biến cố “Quả bóng được chọn ra màu xanh” là: 7, 8, 9, 10 (lấy ra từ tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}).
Do đó, xác xuất của biến cố “Quả bóng được chọn ra màu xanh” là: \(\frac{4}{{10}} = \frac{2}{5}\).
Câu 20:
 Xem đáp án
Xem đáp án
Lời giải
Trong số các quả bóng được chọn, có 5 quả được đánh số chẵn là: 2, 4, 6, 8, 10.
Vậy có 5 kết quả thuận lợi cho biến cố “Quả bóng được chọn ra ghi số chẵn” là: 2, 4, 6, 8, 10, (lấy ra từ tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}).
Do đó, xác xuất của biến cố “Quả bóng được chọn ra ghi số chẵn” là: \(\frac{5}{{10}} = \frac{1}{2}\).
Câu 21:
 Xem đáp án
Xem đáp án
Lời giải
Trong số các quả bóng được chọn, có 3 quả màu vàng ghi số chẵn là: 2, 4, 6.
Vậy có 3 kết quả thuận lợi cho biến cố “Quả bóng được chọn ra màu vàng và ghi số chẵn” là: 2, 4, 6 (lấy ra từ tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}).
Do đó, xác xuất của biến cố “Quả bóng được chọn ra màu vàng và ghi số chẵn” là: \(\frac{3}{{10}}.\)
Câu 22:
Một câu lạc bộ ngoại ngữ có 60 học sinh trong đó có 40 học sinh học tiếng Anh, 30 học sinh học tiếng Pháp, 20 học sinh học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một học sinh trong câu lạc bộ. Tính xác suất của các biến cố sau:
“Học sinh được chọn học tiếng Anh”;
 Xem đáp án
Xem đáp án
Lời giải
Có 40 học sinh học tiếng Anh trong tổng số 60 học sinh.
Do đó, xác suất của các biến cố “Học sinh được chọn học tiếng Anh” là: \(\frac{{40}}{{60}} = \frac{2}{3}\).
Câu 23:
 Xem đáp án
Xem đáp án
Có 30 học sinh học tiếng Anh trong tổng số 60 học sinh
Do đó, xác suất của các biến cố “Học sinh được chọn học tiếng Pháp” là: \(\frac{{30}}{{60}} = \frac{1}{2}\).
Câu 24:
 Xem đáp án
Xem đáp án
Có 20 học sinh học cả tiếng Anh và tiếng Pháp trong tổng số 60 học sinh
Do đó, xác suất của các biến cố “Học sinh được chọn học cả tiếng Anh và tiếng Pháp” là: \(\frac{{20}}{{60}} = \frac{1}{3}\).
