Cho đoạn mạch như hình vẽ:
R1= 6 Ω , R2= 4 Ω. Đèn ghi 6 V- 9 W (bỏ qua điện trở dây nối)
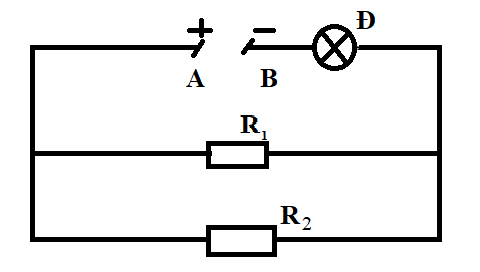
Đặt vào hai đầu đoạn mạch AB một hiệu điện thế không đổi bằng 9 V.
Giải bởi Vietjack
Tóm tắt:
R1= 6\(\Omega \); R2= 4\(\Omega \)
Udm= 6V; Pdm= 9W
U = 9V
Hỏi:
a. RN= ?
b. t = 32 phút, W = ?
c. Đèn sáng bình thường, R2= ?
Lời giải:
Mạch ngoài gồm: Rđnt (R1//R2)
a) Ta có: \({R_d} = \frac{{U_{dm}^2}}{{{P_{dm}}}} = \frac{{{6^2}}}{9} = 4\Omega \)
\({R_{12}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{6.4}}{{6 + 4}} = 2,4\Omega \)
Vậy điện trở của đoạn mạch AB là: RN= Rđ+ R12= 4 + 2,4 = 6,4\(\Omega \)
b) Ta có: t = 32 phút = 1920 giây
Điện năng tiêu thụ trên đoạn mạch AB sau 32 phút là:
\(W = \frac{{{U^2}}}{{{R_N}}}.t = \frac{{{9^2}}}{{6,4}}.1920 = 24300\,J\)
c) Cường độ dòng điện định mức của bóng đèn: \({I_{dm}} = \frac{{{P_{dm}}}}{{{U_{dm}}}} = \frac{9}{6} = 1,5A\)
Để đèn sáng bình thường thì:
Iđ = Idm = 1,5A;
Uđ= Udm= 6V
Cường độ dòng điện qua mạch chính là: Ic = Iđ= 1,5A
Cường độ dòng điện qua đoạn mạch (R1//R2) là: I12= Ic= 1,5 A
Hiệu điện thế đoạn mạch (R1//R2) là: U12 = U– Uđ= 9 – 6 = 3V
Ta có:
\({R_{12}} = \frac{{{U_{12}}}}{{{I_{12}}}} \Leftrightarrow \frac{1}{{{R_{12}}}} = \frac{{{I_{12}}}}{{{U_{12}}}} \Leftrightarrow \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} = \frac{{{I_{12}}}}{{{U_{12}}}}\)
\( \Leftrightarrow \frac{1}{6} + \frac{1}{{{R_2}}} = \frac{{1,5}}{3} \Leftrightarrow {R_2} = 3\Omega \)
Vậy để đèn sáng bình thường thì R2= 3\(\Omega \)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Nhận định nào sau đây không đúng về đường sức của điện trường gây bởi điện tích Q < 0 </>
Hai điện tích \[{q_1} = - {2.10^{ - 8}}C;{q_2} = {3.10^{ - 8}}C\] đặt tại 2 điểm A và B cách nhau 20 cm trong chân không. Tính cường độ điện trường tổng hợp tại N với N nằm trên AB và AN = 40 cm; BN = 60 cm
![Hai điện tích \[{q_1} = - {2.10^{ - 8}}C;{q_2} = {3.10^{ - 8}}C\] đặt tại 2 điểm A và B cách nhau 20 cm trong chân không. Tính cường độ điện trường tổng hợp tại N với N nằm trên AB và AN = (ảnh 1)](https://video.vietjack.com/upload2/images/1647662639/1647662805-image1.png)
Trường hợp nào dưới đây, ta không có một tụ điện? Giữa hai bản kim loại đặt song song và cách nhau một khoảng nhỏ là
