Theo ông Phạm Giang Linh, các đơn vị giáo dục trực tuyến cần thu hút người học bằng cách nào?

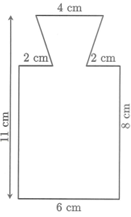
Một thiết bị kỹ thuật là một khối tròn xoay. Mặt cắt của khối tròn xoay đó qua trục của nó được mô tả trong hình bên. Thể tích của thiết bị đó bằng

Tầm quan trọng của nghiên cứu khoa học cơ bản đã thể hiện rõ nét hơn bao giờ hết trong những tháng ngày của năm 2020 khi đại dịch Covid-19 đang hoành hành trên khắp thế giới. Nhờ có các nghiên cứu cơ bản, cụ thể là các nghiên cứu khám phá về virus, con người đã nhanh chóng xác định được các đặc trưng cơ bản cũng như cách chúng phát triển, lây lan và tấn công cơ thể con người. Từ đó, các chính phủ, dựa trên các khuyến nghị từ các nhà khoa học, đã đưa ra các phương án kịp thời và hiệu quả để bảo vệ người dân như giãn cách xã hội hay đeo khẩu trang ở nơi công cộng.

Tuy nhiên, đó chỉ là các phương án tạm thời. Thế giới cần có biện pháp hiệu quả và bền vững hơn, và đó chính là vaccine. Các phương pháp chế tạo vaccine truyền thống cần một thời gian tương đối dài, cỡ 10 năm, và do đó không đáp ứng được nhu cầu cấp bách hiện nay. Rất may, các nghiên cứu khoa học đột phá về mRNA của nhà khoa học người Hungary, TS. Katalin Kariko, tiến hành vào năm 2005 khi bà làm việc tại Đại học Pennsylvania, đã trở thành chìa khóa để giúp các nhà nghiên cứu của Công ty BioNTech, có trụ sở tại thành phố Mainz, nước Đức tìm ra vaccine chỉ trong vòng một thời gian kỷ lục 10 tháng, thay vì 10 năm.

Trước khi Covid-19 nổ ra, các nghiên cứu của TS. Katalin Kariko từng bị hoài nghi. Có lẽ chính TS. Katalin Kariko cũng không thể nghĩ được rằng các nghiên cứu táo bạo của mình lại trở thành phép màu cho cả thế giới 15 năm sau. Như nhà khoa học đoạt giải Nobel về Sinh lý học và Y học năm 1993, Richard Roberts, đã từng nói “Vẻ đẹp của nghiên cứu khoa học thể hiện ở chỗ bạn không bao giờ biết được nó sẽ dẫn đến đâu”. Hay như nhà khoa học đoạt giải Nobel Vật lý năm 2012, Serge Haroche, đã từng nói “Ngay cả những  người thông minh nhất cũng không thể hình dung ra hết các hệ quả của nghiên cứu mà họ tiến hành”. Trong số hàng trăm nghiên cứu lớn nhỏ của TS. Katalin Kariko, chỉ cần một trong số chúng nhen nhóm hi vọng hồi sinh cho cả thế giới thì còn gì tuyệt vời hơn?

Từ câu chuyện về vaccine Covid-19, chúng ta thấy rằng cần phải có một tư duy hệ thống, sâu sắc và dài hạn cho nghiên cứu cơ bản. Nghiên cứu cơ bản là các nghiên cứu đi sâu vào tìm hiểu bản chất và quy luật vận động của các sự vật, hiện tượng tự nhiên. Các kết quả của nó mang tính nguyên bản. Động lực để phát triển nó đó chính là sự tò mò của con  người. Mọi quá trình nóng vội mang tính thời vụ đều không phù hợp với các nghiên cứu cơ bản.

Khi Newton nghiên cứu và xây dựng nên lý thuyết hấp dẫn, mục tiêu của ông đó là giải thích được câu hỏi “tại sao quả táo rơi xuống đất thay vì bay lên trời?”. Nhưng sau đó, chính ông và nhiều nhà khoa học khác thấy được lý thuyết hấp dẫn này còn giải thích và tiên đoán được vô số hiện tượng khác xảy ra trong tự nhiên và vũ trụ. Cơ học Newton đã thành nền tảng lý thuyết để các kỹ sư chế tạo nên máy móc, phương tiện giao thông, cầu đường, nhà cửa. Thiếu nó, mọi hoạt động con người sẽ không còn trơn tru và hiệu quả. Thiếu nó, bạn sẽ không có một chiếc xe Vinfast chạy nhanh và êm ái được.

Khi Planck đề xuất thuyết lượng tử, mục tiêu của ông đó là giải quyết vấn đề chưa có lời giải về phổ bức xạ của vật đen tuyệt đối. Và chắc chắn ông không thể hình dung lý thuyết của mình trở thành một trong hai trụ cột chính của Vật lý hiện đại. Nhờ có lý thuyết lượng tử mà con người ngày hôm nay có các máy tính cá nhân, các điện thoại thông minh, hay các tấm pin năng lượng mặt trời. Nhờ có thuyết lượng tử mà chúng ta có thời đại công nghiệp 4.0. Thiếu nó chúng ta không thể có các tập đoàn công nghệ lớn mạnh như Viettel.

Vào thời điểm này, đại dich Covid-19 vẫn là câu chuyện đang rất nóng hổi. Chúng ta nên biết rằng nếu không có các nghiên cứu khám phá về cấu trúc DNA đầu tiên của Francis Crick, James Watson, và Rosalind Franklin cách đây 67 năm thì chúng ta sẽ không có vaccine Covid-19 nhanh như bây giờ. Chúng ta cần nhớ có rất nhiều loại virus khác nhau tồn tại trong tự nhiên. Hôm nay virus này đến từ con dơi, nhưng ngày mai virus khác có khi lại đến từ một con chim hót rất hay. Chúng ta cần phải chuẩn bị cho các đại dịch có thể xảy ra trong tương lai. Đầu tư cho khoa học cơ bản đề duy trì một đội ngũ các nhà khoa học tài năng, am tường các tiến bộ khoa học – công nghệ của nhân loại là một cách chuẩn bị khôn ngoan nhất. Trong quá khứ, một dân tộc thiện chiến có thể thống lĩnh cả thế giới. Nhưng trong tương lai, một dân tộc tồn tại được dài lâu hay không phụ thuộc vào việc dân tộc đó uyên bác đến mức độ nào.

Một đoàn tàu gồm 12 toa chở khách. Có 7 hành khách chuẩn bị lên tàu. Tính xác suất để đúng 3 toa có người.

Xét các số phức z thỏa mãn $\frac{z-2+5i}{\left(z+\overline{z}\right)i+2}$  là số thực. Tập hợp các điểm biểu diễn của số phức 2z là một parabol (P). Tính diện tích hình phẳng giới hạn bởi (P)và trục hoành.

Ông An muốn xây một bể chứa nước dạng hình hộp chữ nhật, phần nắp trên ông để trống một ô có diện tích bằng 20% diện tích của đáy bể. Biết đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng, bể có thể tích tối đa 10m³ nước và giá tiền thuê nhân công 500 000 đồng/m³. Số tiền ít nhất mà ông phải trả cho nhân công gần nhất với đáp án nào dưới đây?

Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân, $AB=AC=a,AA\text{'}=a\sqrt{3}$. Tính khoảng cách giữa hai đường thẳng chéo nhau   AB', BC'

Cho hình chóp S.ABCD có ABCD là hình chữ nhật tâm I cạnh AB = 3a; BC = 4a. Hình chiếu của S trên mặt phẳng (ABCD) là trung điểm của ID. Biết rằng SB tạo với mặt phẳng (ABCD) một góc 45^o. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD

Cho hình chóp S.ABC có $\widehat{BAC}={90}^o,AB=3a,AC=4a.$ Hình chiếu của đỉnh S là một điểm H nằm trong tam giác ABC. Biết khoảng cách giữa các cặp đường thẳng chéo nhau của hình chóp là $d\left(SA,BC\right)=\frac{6a\sqrt{34}}{17},d\left(SB,CA\right)=\frac{12a}{5},d\left(SC,AB\right)=\frac{12a\sqrt{13}}{13}.$ Tính thể tích khối chóp S.ABC.

Cho số phức $z=m+3+\left(m^2-m-6\right)i$ với $m\in ℝ$. Gọi (P) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC vuông tại C, $\widehat{ABC}={60}^o,AB=3\sqrt{2}$ đường thẳng AB có phương trình $\frac{x-3}{1}=\frac{y-4}{1}=\frac{z+8}{-4},$ đường thẳng AC nằm trên mặt phẳng $\left(\alpha \right):x+z-1=0.$ Biết B là điểm có hoành độ dương. Gọi (a; b; c) là tọa độ điểm C, giá trị của a + b + c bằng

Thông tin nào sau đây KHÔNG chính xác?