A.
B.
C.
D. (0;1)
 Giải bởi Vietjack
Giải bởi Vietjack
Lấy loganepe hai vế ta có
Vì
Vậy tập nghiệm của bất phương trình là
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số y = f(x). Hàm số y = f′(x) có bảng biến thiên như sau:
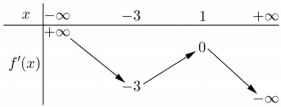
Bất phương trình đúng với mọi khi và chỉ khi: