Cho khối lăng trụ tam giác đều ABC.A′B′C′. Các mặt phẳng (ABC′) và (A′B′C) chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu H1, H2 lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Giá trị của bằng
A.4
B.2
C.5
 Giải bởi Vietjack
Giải bởi Vietjack
Bước 1:
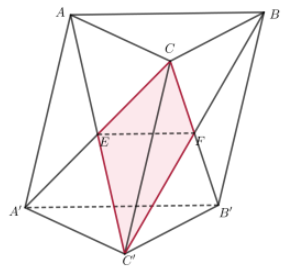
Gọi E là giao điểm của AC và AC’ và F là giao điểm của BC’ và B’C’
Khi đó (ABC’) và (A’B’C) chia khối lăng trụ tam giác đều ABC.A’B’C’ thành 4 khối đa diện: CEFC’;FEA’B’C’;FEABC và FEABB’A’
Gọi V là thể tích của khối lăng trụ tam giác đều ABC.A’B’C’.
Bước 2: Tính thể tích của và theo thể tích của
Ta có
và
Mặt khác
Do đó có thể tích lớn nhất là khối đa diện FEABB’A’; có thể tích nhỏ nhất là khối đa diện CEFC’ và
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Đề thi THPT QG - 2021 - mã 101
Cho khối hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông, , góc giữa hai mặt phẳng (A′BD) và (ABCD) bằng 300. Thể tích của khối hộp chữ nhật đã cho bằng
Cho hình lăng trụ ABCD.A′B′C′D′ có đáy ABCD là hình thoi cạnh a và góc . Chân đường cao hạ từ B′ xuống (ABCD) trùng với giao điểm 2 đường chéo, biết . Thể tích khối lăng trụ là:
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là tứ giác đều cạnh a, biết rằng . Tính thể tích của khối lăng trụ?
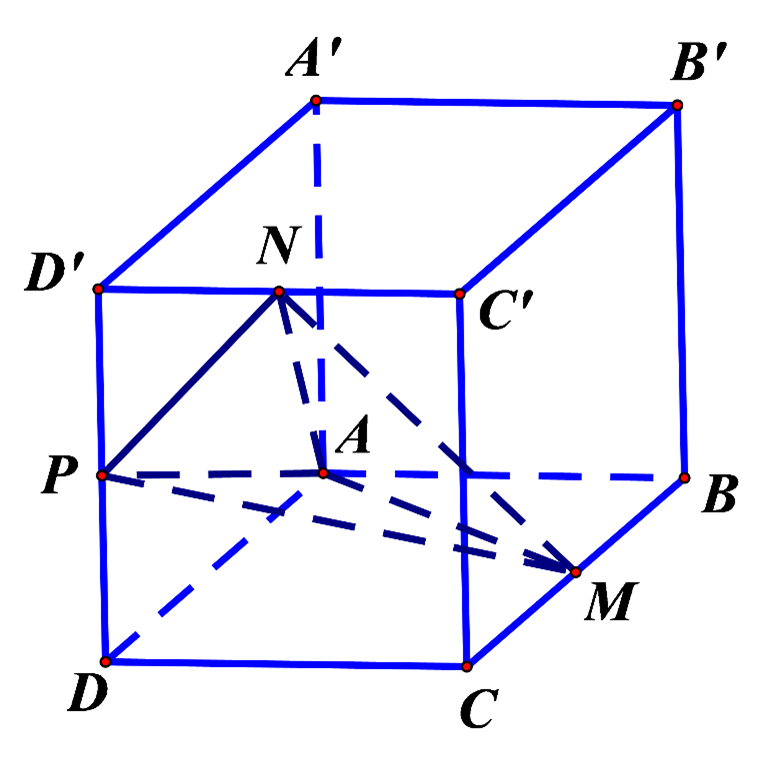
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có độ dài cạnh đáy , cạnh bên bằng (minh họa như hình vẽ). Gọi M là trung điểm của cạnh A′C′. Khoảng cách từ B′ đến mặt phẳng (ABM) bằng bao nhiêu?
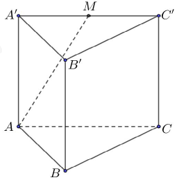
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác cân và AB′ vuông góc với . Mặt phẳng tạo với mặt phẳng một góc 300. Thể tích khối lăng trụ ABC.A′B′C′ là:
Cho lăng trụ xiên tam giác ABC.A′B′C′ có đáy ABC là tam giác đều cạnh a, biết cạnh bên là và hợp với đáy ABC một góc 600. Thể tích khối lăng trụ là:
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy ABC là tam giác vuông tại , cạnh BC=a, đường chéo A′B tạo với mặt phẳng (ABC) một góc 300. Thể tích khối lăng trụ ABC.A′B′C′ là:
Cho hình lăng trụ tam giác ABC.A′B′C′ có diện tích đáy bằng 12 và chiều cao bằng 6. Gọi M,N lần lượt là trung điểm của CB,CA và P,Q,R lần lượt là tâm các hình bình hành ABB′A′, BCC′B′, CAA′C′. Thể tích của khối đa diện PQRABMN bằng:
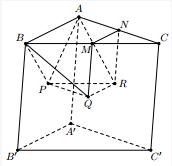
Cho lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh a, và . Thể tích khối lăng trụ ABC.A′B′C′ theo a là:
Ông A dự định sử dụng hết 5m2 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Cho hình lăng trụ ABC.A′B′C′ có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C trên (ABB′A′) là tâm của hình bình hành ABB′A′. Thể tích của khối lăng trụ là:
Cho lăng trụ đều ABC.A′B′C′, cạnh đáy bằng a, góc giữa hai mặt phẳng và (ABC) bằng 600. Tính thể tích khối lăng trụ đó.