Cho tam giác OAB và điểm D nằm trên cạnh AB thỏa mãn ∆OAD = ∆OBD (hình vẽ).
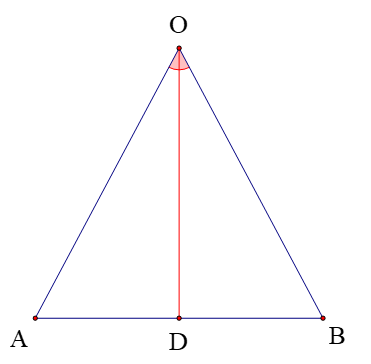
Nhận định nào dưới đây sai?
A. D là trung điểm của đoạn thẳng AB;
B. OD là tia phân giác của góc AOB;
C. OD ⊥ AB;
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Vì ∆OAD = ∆OBD (giả thiết)
Nên (các góc tương ứng bằng nhau)
Và OA = OB; AD = BD (các cạnh tương ứng bằng nhau)
Vì AD = BD và D thuộc AB nên D là trung điểm của đoạn thẳng AB.
Vì và tia OD nằm giữa 2 tia OA và OB nên OD là tia phân giác của góc AOB.
Vì mà (hai góc kề bù)
Suy ra
Do đó tam giác OAD và tam giác OBD là tam giác vuông. OD ⊥ AB.
Vậy D là khẳng định sai.
Gói VIP thi online tại VietJack (chỉ 200k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
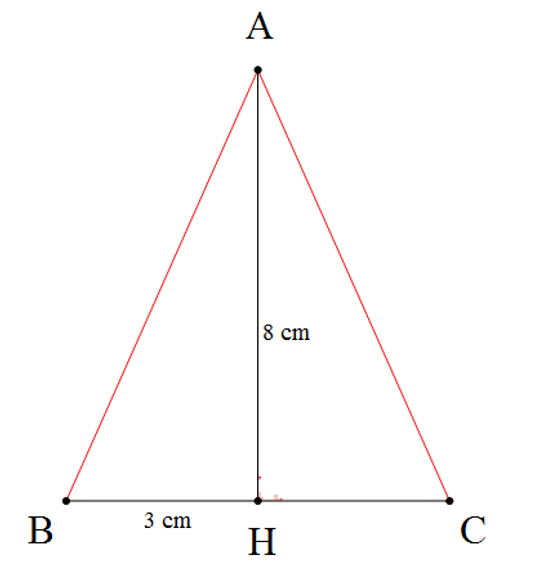
Cho ∆ABH = ∆ACH (hình vẽ). Biết AH = 8 cm, BH = 3 cm. Diện tích tam giác AHC là
