5 câu hỏi trắc nghiệm thuộc Đề số 01

Đề thi Toán 7 Giữa kì 1 (có đáp án)

Đề số 01

5210 lượt thi
5 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

(2,0 điểm) Tính:

$a) 0, 5 + \frac{3}{16} - \frac{- 3}{4};$ $b) \frac{2}{3} - (2 - \frac{1}{3}) + \frac{3}{2} + (0, 75) °;$

$c) \frac{5}{4} - \frac{5}{6} : (\frac{3}{8} - \frac{1}{6}) + \frac{11}{12};$ $d) {(\frac{2}{3})}^{3} : {(\frac{2}{3})}^{2} + (- 1 \frac{1}{2}) : 1, 5;$

Xem đáp án

$a) 0, 5 + \frac{3}{16} - \frac{- 3}{4} = \frac{8}{16} + \frac{3}{16} + \frac{12}{16} = \frac{11}{16} + \frac{12}{16} = \frac{23}{16} .$

$b) \frac{2}{3} - (2 - \frac{1}{3}) + \frac{3}{2} + (0, 75) ° = \frac{2}{3} - (\frac{6}{3} - \frac{1}{3}) + \frac{3}{2} + 1 = \frac{2}{3} - \frac{5}{3} + \frac{3}{2} + 1 = \frac{- 3}{3} + \frac{3}{2} + 1 = - 1 + \frac{3}{2} + 1 = (- 1 + 1) + \frac{3}{2} = 0 + \frac{3}{2} = \frac{3}{2} .$

$c) \frac{5}{4} - \frac{5}{6} : (\frac{3}{8} - \frac{1}{6}) + \frac{11}{12} = \frac{5}{4} - \frac{5}{6} : (\frac{9}{24} - \frac{4}{24}) + \frac{11}{12} = \frac{5}{4} - \frac{5}{6} : \frac{5}{24} + \frac{11}{12} = \frac{5}{4} - \frac{5}{6} . \frac{24}{5} + \frac{11}{12} = \frac{5}{4} - 4 + \frac{11}{12} = \frac{15}{12} - \frac{48}{12} + \frac{11}{12} = \frac{- 33}{12} + \frac{11}{12} = \frac{- 22}{12} = \frac{- 11}{6} .$

$d) {(\frac{2}{3})}^{3} : {(\frac{2}{3})}^{2} + (- 1 \frac{1}{2}) : 1, 5 = \frac{2}{3} + \frac{- 3}{2} : \frac{3}{2} = \frac{2}{3} + \frac{- 3}{2} . \frac{2}{3} = \frac{2}{3} - 1 = \frac{2}{3} - \frac{3}{3} = \frac{- 1}{3} .$

Câu 2:

(2,0 điểm) Tìm x biết:

$a) 2 x = 3 y v à x y = 54;$ $b) \frac{x}{8} = \frac{y}{5} = \frac{z}{6} v à 2 x + y - z = - 30;$

Xem đáp án

$a) T a c ó : 2 x = 3 y \Rightarrow x = \frac{3}{2} y . T h a y x = \frac{3}{2} y v à o x y = 54 t a đ ư ợ c : \frac{3}{2} y . y = 54 \Rightarrow y^{2} = 54 : \frac{3}{2} \Rightarrow y^{2} = 36 \Rightarrow y = 6 h o ặ c y = - 6 V ớ i y = 6 t a c ó x = \frac{3}{2} . 6 = 9 V ớ i y = - 6 t a c ó x = \frac{3}{2} . (- 6) = - 9 V ậ y c ặ p g á i t r ị (x; y) c ầ n t ì m l à (9; 6) v à (- 9; - 6)$

$b) \frac{x}{8} = \frac{y}{5} = \frac{z}{6} v à 2 x + y - z = - 30 T h e o b à i r a t a c ó : \frac{x}{8} = \frac{y}{5} = \frac{z}{6} = \frac{2 . x + y - z}{2.8 + 5 - 6} = \frac{- 30}{15} = - 2 (á p d ụ n g t í n h c h ấ t d ã y t ỉ s ố b ằ n g n h a u) K h i đ ó t a c ó : \frac{x}{8} = - 2 \Rightarrow x = - 2.8 \Rightarrow x = - 16 \frac{y}{5} = - 2 \Rightarrow y = - 2.5 \Rightarrow y = - 10 \frac{z}{6} = - 2 \Rightarrow z = - 2.6 \Rightarrow z = - 12 V ậ y x = - 16; y = - 10; z = - 12$

Câu 3:

(2,0 điểm) Hưởng ứng phong trào khuyên góp sách, ba lớp 7A, 7B, 7C đã khuyên góp được tổng số 180 cuốn sách. Biết số cuốn sách của 3 lớp 7A, 7B, 7C tỉ lệ với các số 5;6;4 . Tính số sách mà mỗi lớp đã khuyên góp được.

Xem đáp án

Gọi số sách mà ba 7A, 7B, 7C lớp khuyên góp được lần lượt là x;y;z $(x; y; z \in ℕ *)$

Vì số cuốn sách của 3 lớp 7A, 7B, 7C tỉ lệ với các số 5;6;4 ta có: $\frac{x}{5} = \frac{y}{6} = \frac{z}{4} .$

Vì đã khuyên góp được tổng số 180 cuốn sách nên: x+y+z=180

Ta có: $\frac{x}{5} = \frac{y}{6} = \frac{z}{4} = \frac{x + y + z}{5 + 6 + 4} = \frac{180}{15} = 12$ (áp dụng tính chất dãy tỉ số bằng nhau)

Khi đó ta có:

$\frac{x}{5} = 12 \Rightarrow x = 12.5 \Rightarrow x = 60$ (TM)

$\frac{y}{6} = 12 \Rightarrow y = 12.6 \Rightarrow y = 72$ (TM)

$\frac{z}{4} = 12 \Rightarrow z = 12.4 \Rightarrow z = 48$ (TM)

Vậy số sách mà ba lớp 7A, 7B, 7C khuyên góp được lần lượt là 60;72;48 cuốn sách.

Câu 4:

(3,5 điểm) Vẽ lại hình và chú thích đầy đủ

Cho hình vẽ. Biết $\hat{M N p} = 62 °; \hat{N M a} = 118 °; \hat{Q P b} = 152 °$

a ) Chứng minh aa' // bb' ;

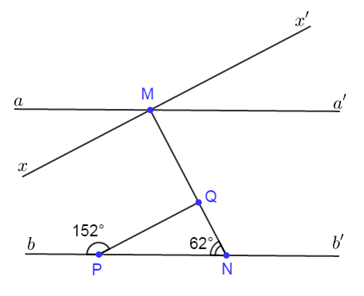
b) Tính số đo góc MQP. Trên nữa mặt phẳng bờ aa' chứa điểm N, vẽ tia Mx // QP. Tính số đo góc aMx;

c) Trên nữa mặt phẳng bờ aa' không chứa điểm N vẽ tia Mx' sao cho

\hat{a M x} = \hat{a' M x'}

. Chứng minh hai tia Mx và Mx' là hai tia đối nhau.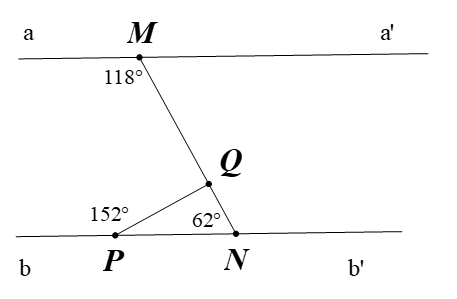

Vẽ lại hình và chú thích đầy đủ a ) Chứng minh aa' // bb' (ảnh 1)

Xem đáp án

a. Vì $\hat{M N b} + \hat{N M a} = 62 ° + 118 ° = 180 °$ mà hai góc này ở

vị trí trong cùng phía nên aa' // bb' (dấu hiệu nhận biết)

b. Ta có: $\hat{Q P b} + \hat{Q P N} = 180 ° \Rightarrow \hat{Q P N} = 180 ° - \hat{Q P b} = 28 °$ (hai góc bù nhau)

Ta có : $\hat{M Q P} = \hat{Q P N} + \hat{Q N P} = 28 ° + 62 ° = 90 °$ (tính chất góc ngoài tam giác)

Vì Mx // QP và $\hat{M Q P} = 90 °$ suy ra $\hat{x M Q} = 90 °$ (quan hệ song song và vuông góc)

Từ đó: $\hat{a M x} = 118 ° - \hat{x M Q} = 118 ° - 90 ° = 28 °$

c. Ta có: $\hat{a M x} + \hat{x M a'} = 180 ° \Rightarrow \hat{a M x} + \hat{x' M a'} = 180 ° \Rightarrow \hat{x M x'} = 180 °$ hay Mx và Mx’ là hai tia đối nhau.

Câu 5:

(0,5 điểm) Học sinh chỉ chọn một trong hai ý sau :

a) Cho các số a,b,c thỏa mãn $a . b . c \neq 0$ và $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{a + b}{c} + \frac{b + c}{a} + \frac{c + a}{b} = \frac{1}{3}$ .

Tính S= a+b+c+2020.

b) Tìm các số a,b,c nguyên dương thỏa mãn: $a^{3} + 3 a^{2} + 5 = 5^{b}$ và $a + 3 = 5^{c}$ .

Xem đáp án

a) Ta có: $\frac{a + b}{c} + \frac{b + c}{a} + \frac{c + a}{b} = \frac{1}{3}$

$\Leftrightarrow \frac{a + b}{c} + 1 + \frac{b + c}{a} + 1 + \frac{c + a}{b} + 1 = \frac{1}{3} + 3$

$\Leftrightarrow \frac{a + b + c}{c} + \frac{a + b + c}{a} + \frac{a + b + c}{b} = \frac{10}{3}$

$\Leftrightarrow (a + b + c) (\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) = \frac{10}{3}$

$\Leftrightarrow a + b + c = 10$

Thay vào đó ta được S= 10+2020=2030.

b) Ta có: $a^{3} + 3 a^{2} + 5 = 5^{b}$

$\Leftrightarrow a^{2} (a + 3) + 5 = 5^{b}$

$\Leftrightarrow a^{2} . 5^{c} = 5^{b}$ (3)

Xét:

TH1: c=1 thay vào (2) ta có a=2, khi đó thay tiếp vào (1) ta được b=2.

TH2: khi đó từ (3) suy ra b>1 nhưng sẽ vô lý vì cả $a^{2} . 5^{c}; 5^{b}$ đều chia hết cho $5^{2}$ mà 5 thì không.

Vậy a=2; b=2; c=1.

Bắt đầu thi ngay

Bài thi liên quan

Đề số 02
- 8 câu hỏi
- 45 phút
Đề số 03
- 13 câu hỏi
- 60 phút
Đề số 04
- 4 câu hỏi
- 60 phút
Đề số 05
- 5 câu hỏi
- 60 phút
Đề số 06
- 10 câu hỏi
- 60 phút
Đề sô 07
- 9 câu hỏi
- 60 phút
Đề số 08
- 10 câu hỏi
- 60 phút
Đề số 09
- 10 câu hỏi
- 60 phút
Đề số 10
- 8 câu hỏi
- 60 phút
Đề số 11
- 8 câu hỏi
- 60 phút

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Toán 7 Giữa kì 1 (có đáp án)

Đề số 01

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương