Cho tam giác ABC, đường trung tuyến BD, trên tia đối của tia DB lấy điểm E sao cho DE = DB, gọi M, N theo thứ tự là trung điểm của BC và CE. Gọi I, K theo thứ tự là giao điểm của AM, AN với BE. Nhận định đúng nhất là
A. BI = KE;
B. BI = IK;
C. BI = IK = KE;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
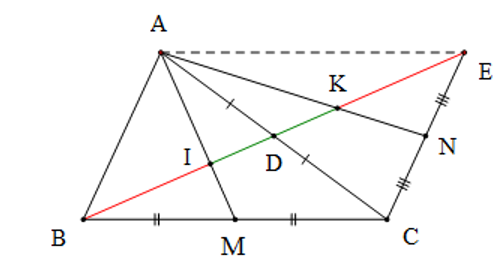
M là trung điểm của BC nên AM là trung tuyến của tam giác ABC.
Tam giác ABC có hai đường trung tuyến AM và BD cắt nhau tại I ⇒ I là trọng tâm tam giác ABC.
Do đó: và
Mặt khác, N là trung điểm của CE nên AN là trung tuyến của tam giác ACE.
Tam giác ACE có hai đường trung tuyến AN và ED cắt nhau tại K ⇒ K là trọng tâm tam giác ACE.
Do đó: và .
Mà BD = DE (giả thiết)
Do đó : BI = IK = KE .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho ∆ABC vuông tại A. Trung tuyến AK và BH cắt nhau tại M. Trên tia đối của tia KA lấy D sao cho KD = KA. DH cắt BC tại N. Kết luận nào dưới đây sai?
Cho hình vẽ sau
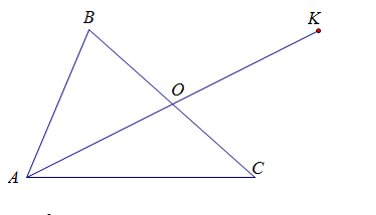
Biết rằng AO là đường trung tuyến của ∆ABC, AO = OK; AB = 6,3 cm; BC = 6,5 cm; AC = 6,7 cm. Độ dài CK bằng