Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB =a vuông góc với mặt phẳng đáy. Biết rằng khoảng cách giữa BD và SC bằng . Tính khoảng cách d từ B đến mặt phẳng (SCD)
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
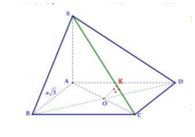
Gọi O = AC BD Kẻ OK SC Do BD (SAC) =>BDOK
Do đó d(BC;SC) =OK=
Khi đó: Kẻ AH SD => AH (SDC) => AH =d(A;(SCD))
Lại có AB//CD => AB //(SCD) => d(B;(SCD))= d(A;(SCD)=AH
vuông tại A có
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian, cho hình chữ nhật ABCD có AB= 1 và AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ (tham khảo hình vẽ bên). Tính diện tích toàn phần của hình trụ đó.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 48. Gọi M,N lần lượt là điểm thuộc các cạnh AB, CD sao cho MA=MB, NC =2ND . Tính thể tích V của khối chóp S.MBCN
Gọi l, h , R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Đẳng thức nào sau đâu đúng?
Cho hình lập phương ABCD.A’B’C’D’. I là trung điểm BB’. Mặt phẳng (DIC’) chia khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng:
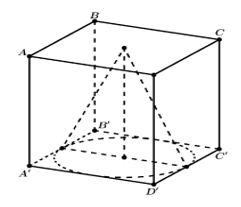
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuôngA'B'C'D'. Kết quả tính diện tích toàn phần của khối nón đó có dạng với b và c là hai số nguyên dương và b>1. Tính bc
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB =3a, AC = 4a, AD=5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
Cho hình lăng trụ tam giác đều có cạnh đáy bằng 2a và có các mặt bên đều là hình vuông. Thể tích khối lăng trụ đã cho bằng
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a cạnh bên SA = a và vuông góc với đáy. Côsin góc giữa đường thẳng SC và mặt (SBD) bằng
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 1 cạnh bên hợp với mặt đáy một góc Khoảng cách từ O đến mặt phẳng (SBC) bằng
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C. Gọi H là trung điểm AB. Biết rằng SH vuông góc với mặt phẳng (ABC) và AB =SH =a Tính cosin của góc tọa bởi hai mặt phẳng (SAB) và (SAC).
Cho tứ diện ABCD có BD =3, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 11, số đo góc giữa hai mặt phẳng (ABD) và (BCD) là
Trong tất cả các hình chóp tứ giác đều có d= là khoảng cách giữa hai đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất của khối chóp là
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, BC=a Cạnh bên SA =a và vuông góc với đáy (ABCD) Cosin của góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) bằng
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA = và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC).
Cho hình chóp tứ giác đều S.ABCD có AB = a, gọi là góc giữa mặt bên và mặt đáy của hình chóp S.ABCD. Tính khoảng cách d giữa SA và CD theo a và