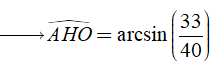Giải SGK Toán 4 CD Bài 38. Chia cho số có một chữ số có đáp án
-
151 lượt thi
-
20 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình lập phương ABCD.A'B'C'D' có cạnh là a. Tính thể tích khối tứ diện ABC'D' theo a?
 Xem đáp án
Xem đáp án
Đáp án D
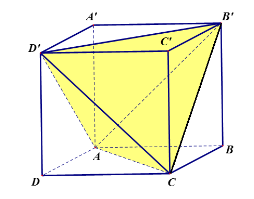

Nhận xét:
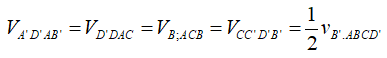

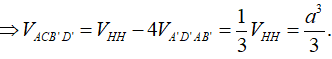
Cách khác:
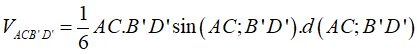
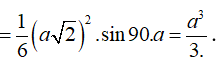
Câu 2:
Cho hình chóp S.ABC có đáy là tam giác vuông tại B,AB =a, AC=a tam giác SAB đều và nằm trong mặt phẳng vuông góc đáy. Gọi a (độ) là bởi cạnh SB và mặt phẳng (SAB). Gía trị a gần với số nào nhất dưới đây?
 Xem đáp án
Xem đáp án
Đáp án C
Gọi H là trung điểm AB
![]()
![]()
Suy ra K là hình chiếu từ H trên (SAC)
Do đó, nếu gọi L là hình chiếu từ B lên (SAC) thì BL=2HK.
![]()
Từ đó, tính được
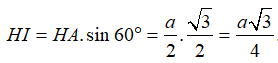
Ta có:
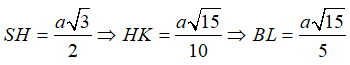
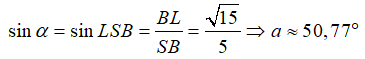
Câu 3:
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB =3a, AC = 4a, AD=5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
 Xem đáp án
Xem đáp án
Đáp án C
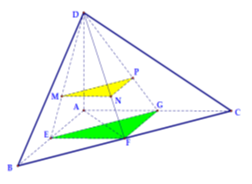
Gọi E,F,G lần lượt là trung điểm của các cạnh AB, BC, AC.
Khi đó:
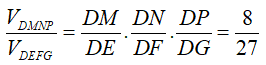
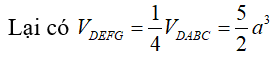

Câu 4:
Cho hình chóp tứ giác đều S.ABCD có AB = a, gọi là góc giữa mặt bên và mặt đáy của hình chóp S.ABCD. Tính khoảng cách d giữa SA và CD theo a và
 Xem đáp án
Xem đáp án
Đáp án C
Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).
Gọi I, K theo thứ tự là trung điểm AB, CD thì:
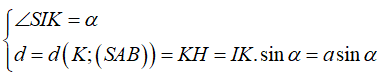
Trong đó H là hình chiếu từ K lên SI
Câu 5:
Cho hình lập phương ABCD.A’B’C’D’. I là trung điểm BB’. Mặt phẳng (DIC’) chia khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng:
 Xem đáp án
Xem đáp án
Đáp án B
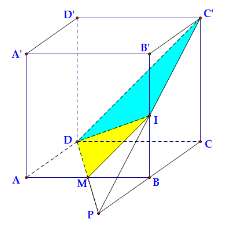
![]()
![]()
Dễ dàng chứng minh B, M lần lượt là trung điểm PC và AB

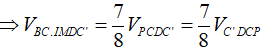
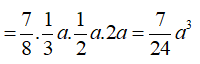
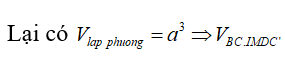
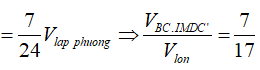
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB =a vuông góc với mặt phẳng đáy. Biết rằng khoảng cách giữa BD và SC bằng . Tính khoảng cách d từ B đến mặt phẳng (SCD)
 Xem đáp án
Xem đáp án
Đáp án C
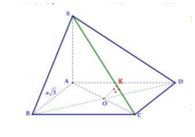
Gọi O = AC BD Kẻ OK SC Do BD (SAC) =>BDOK
Do đó d(BC;SC) =OK=
Khi đó: Kẻ AH SD => AH (SDC) => AH =d(A;(SCD))
Lại có AB//CD => AB //(SCD) => d(B;(SCD))= d(A;(SCD)=AH
vuông tại A có
Câu 7:
Cho hình lăng trụ tam giác đều có cạnh đáy bằng 2a và có các mặt bên đều là hình vuông. Thể tích khối lăng trụ đã cho bằng
 Xem đáp án
Xem đáp án
Chọn B.
Lời giải. Từ giả thiết, ta có
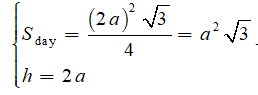
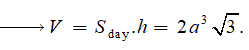
Câu 8:
Trong không gian, cho hình chữ nhật ABCD có AB= 1 và AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ (tham khảo hình vẽ bên). Tính diện tích toàn phần của hình trụ đó.
 Xem đáp án
Xem đáp án
Chọn C.
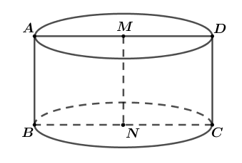
Lời giải. Diện tích xung quanh hình trụ:
![]()
Diện tích hai đáy của của hình trụ:
![]()
Vậy diện tích toàn phần của hình trụ:
![]()
Câu 9:
Cho hình lăng trụ ABC.A'B'C' có các mặt bên đều là hình vuông cạnh a Gọi D, E, F lần lượt là trung điểm của các cạnh BC, A'C', C'B'. Khoảng cách giữa hai đường thẳng DE và AB' bằng
 Xem đáp án
Xem đáp án
Chọn C.
Lời giải.

Từ giả thiết suy ra lăng trụ đã cho là lặng trụ đứng và hai mặt đáy là những tam giác đều cạnh a.
![]()
![]()
Ta chứng minh được DK là đoạn vuông góc chung của DE và AB' nên![]()
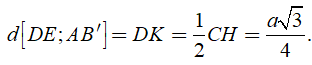
Câu 10:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 1 cạnh bên hợp với mặt đáy một góc Khoảng cách từ O đến mặt phẳng (SBC) bằng
 Xem đáp án
Xem đáp án
Chọn D.
Lời giải. Xác định
![]()

Gọi M là trung điểm BC, kẻ OKSM.
![]()
Tam giác vuông SOM
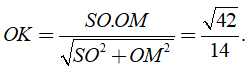
Câu 11:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a cạnh bên SA = a và vuông góc với đáy. Côsin góc giữa đường thẳng SC và mặt (SBD) bằng
 Xem đáp án
Xem đáp án
Chọn D
Lời giải.

Chứng minh được
![]()
![]()
Ta tính được
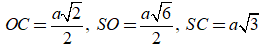
![]()
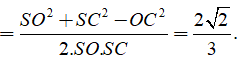
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 48. Gọi M,N lần lượt là điểm thuộc các cạnh AB, CD sao cho MA=MB, NC =2ND . Tính thể tích V của khối chóp S.MBCN
 Xem đáp án
Xem đáp án
Đáp án C
Lời giải.
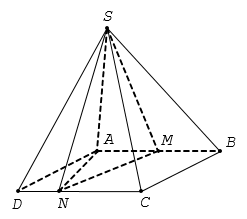
Gọi d là khoảng cách từ đỉnh A đến cạnh CD
Diện tích hình bình hành
Ta có
![]()
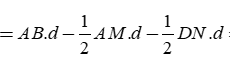

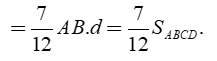

Câu 13:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, BC=a Cạnh bên SA =a và vuông góc với đáy (ABCD) Cosin của góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) bằng
 Xem đáp án
Xem đáp án
Chọn B
Lời giải. Để cho gọn ta chọn a=1
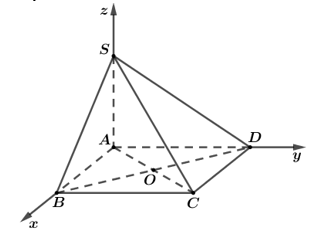
Chọn hệ trục tọa độ Oxyz như hình vẽ với A(0;0;0) và B(1;0;0) , D(0;;0)
Suy ra C(1;;0)
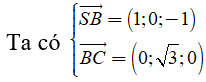
VTPT của mặt phẳng (SBC) là
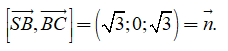
Đường thẳng có VTCP là
![]()
Khi đó
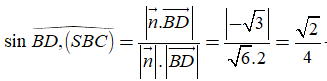

Câu 14:
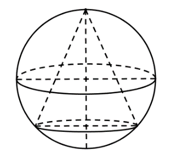
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kì nội tiếp mặt cầu (S) (tham khảo hình vẽ bên). Thể tích khối nón (H) là ; thể tích phần còn lại là . Giá trị lớn nhất của bằng
 Xem đáp án
Xem đáp án
Chọn C
Lời giải.
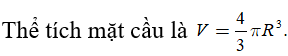
Ta có

Suy ra lớn nhất khi nhỏ nhất => đạt giá trị lớn nhất.
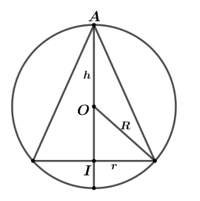
Gọi h,r lần lượt là chiều cao và bán kính đáy của hình nón nội tiếp mặt cầu.
Gọi I, O lần lượt là tâm của đường tròn đáy hình nón và tâm của mặt cầu.
Gọi A là đỉnh của hình nón. Xét thiết diện qua trục của hình nón như hình vẽ bên.
![]()
![]()
Xét hàm
![]()

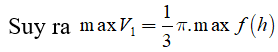

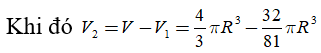
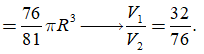
Cách 2.
![]()
TH1. Chiều cao của khối nón h= R + x và bán kính đáy
Theo BĐT Cô si cho 3 số dương, ta có

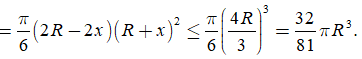
Dấu "=" xảy ra
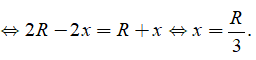
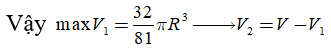
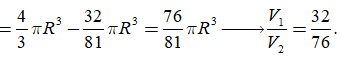
TH2. Chiều cao của khối nón h = R - x. Làm tương tự.
Câu 15:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C. Gọi H là trung điểm AB. Biết rằng SH vuông góc với mặt phẳng (ABC) và AB =SH =a Tính cosin của góc tọa bởi hai mặt phẳng (SAB) và (SAC).
 Xem đáp án
Xem đáp án
Chọn D.
Lời giải.
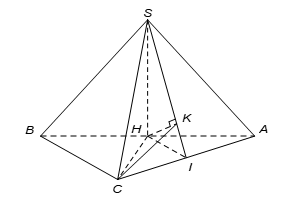
Ta có
![]()
![]()
![]()
Từ (1) và (2)
![]()
Gọi I là trung điểm AC
![]()
Mặt khác
![]()
Từ (3) và (4)
![]()
![]()
![]()
![]()
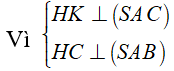
nên góc giữa hai mặt phẳng (SAC) và (SAB) bằng góc giữa hai đường thẳng HK và HC.
Xét tam giác CHK vuông tại K, có

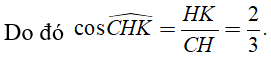
Câu 16:
Trong tất cả các hình chóp tứ giác đều có d= là khoảng cách giữa hai đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất của khối chóp là
 Xem đáp án
Xem đáp án
Chọn B.
Lời giải.

Xét hình chóp tứ giác đều S.ABCD, đặt AB =x, SO =h. Với O là tâm của hình vuông ABCD . Qua O kẻ đường thẳng OH vuông góc với SA với H SA
Ta có
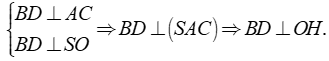
Suy ra OH là đoạn vuông góc chung của SA và BD
Theo bài ra, ta có
![]()
Tam giác SAO vuông tại O, có đường cao OH suy ra
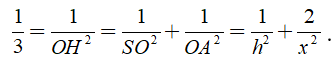
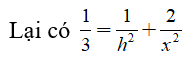
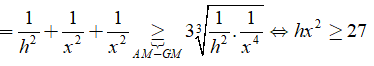
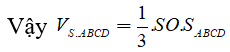
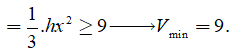
Câu 17:
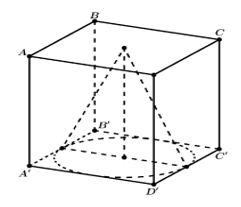
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuôngA'B'C'D'. Kết quả tính diện tích toàn phần của khối nón đó có dạng với b và c là hai số nguyên dương và b>1. Tính bc
 Xem đáp án
Xem đáp án
Chọn A.
Lời giải. Ta có bán kính hình nón r=, đường cao h=a,
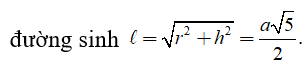
Diện tích toàn phần
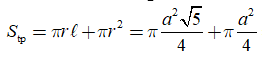
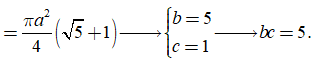
Câu 18:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA = và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC).
 Xem đáp án
Xem đáp án
Chọn A
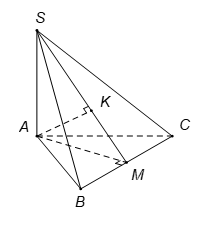
Gọi M là trung điểm BC
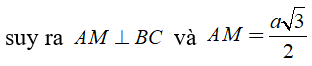
Gọi K là hình chiếu của A trên SM , suy ra AK SM. (1)

![]()
![]()
![]()

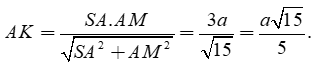

Câu 19:
Cho tứ diện ABCD có BD =3, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 11, số đo góc giữa hai mặt phẳng (ABD) và (BCD) là
 Xem đáp án
Xem đáp án
Chọn A.
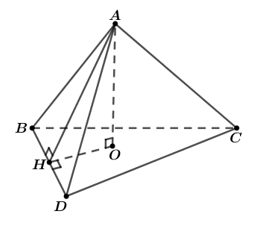
Gọi O là chân đường vuông góc kẻ từ A đến mặt phẳng (BCD)
![]()

![]()
![]()
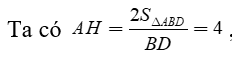
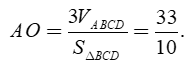
Khi đó ta tính được