Một vật dao động điều hoà dọc theo trục Ox với phương trình: x = Acos(πt) cm. Nếu chọn gốc toạ độ O tại vị trí cân bằng của vật thì gốc thời gian t=0 là lúc vật:

Một con lắc lò xo dao động với phương trình x = 6cos(20πt)cm. Xác định chu kỳ, tần số dao động của chất điểm.   

Vật dao động điều hòa có đồ thị vận tốc - thời gian như hình vẽ. Tần số góc và pha ban đầu của li độ của vật là:

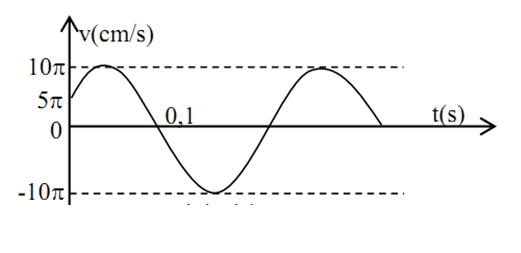
Ta có:

\[\left\{ {\begin{array}{*{20}{c}}{A\omega = 10\pi cm/s}\\{\frac{{5T}}{{12}} = 0,1 \to T = 0,24s \to \omega = \frac{{25\pi }}{3}rad/s}\end{array}} \right.\]

Tại t = 0:

\[\left\{ {\begin{array}{*{20}{c}}{v = 5\pi }\\{v >0}\end{array}} \right. \leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - A\omega \sin \varphi = 5\pi }\\{\sin \varphi < 0}\end{array}} \right. \leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\sin \varphi = \frac{{ - 5\pi }}{{10\pi }} = \frac{{ - 1}}{2}}\\{\sin \varphi < 0}\end{array}} \right.\]

\[ \to \varphi = \left[ {\begin{array}{*{20}{c}}{ - \frac{\pi }{6}}\\{\frac{{7\pi }}{6}}\end{array}} \right.\]

Mặt khác, vận tốc đang tăng \[ \Rightarrow \varphi = \frac{{7\pi }}{6}\]

</>

Một vật dao động điều hoà chu kỳ T. Gọi v_max và a_max tuơng ứng là vận tốc cực đại và gia tốc cực đại của vật. Hệ thức liên hệ sai giữa v_max và a_max  là:

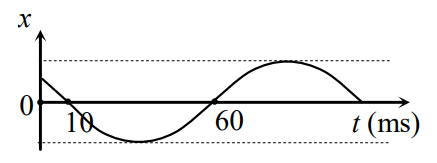
Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là

Một chất điểm dao động điều hoà với phương trình dạng

\[x = 5\cos \left( {7\pi t + \frac{{7\pi }}{6}} \right)cm\]. Biểu thức vận tốc tức thời của chất điểm là:

Một vật dao động điều hòa có biên độ là 2(cm) và  tần số góc \[\omega = 2\pi \left( {rad} \right)\]. Lấy \[{\pi ^2} = 10\], gia tốc của vật tại thời điểm vật có vận tốc \[v = 2\sqrt 3 \pi cm/s\]là:

^A.40cm/s²

^B.80cm/s²

^C.±40cm/s²

^D.±80cm/s²

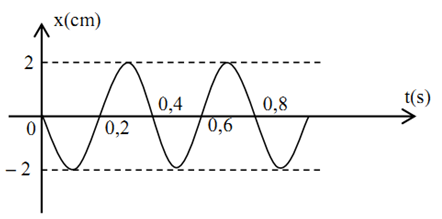
Một chất điểm dao động điều hoà với phương trình dạng

\[x = \cos \left( {2\pi t + \frac{\pi }{6}} \right)\left( {cm,s} \right)\]. Lấy π² = 10, biểu thức gia tốc tức thời của chất điểm là:

Một đĩa phẳng nhẵn nằm ngang, chuyển động tròn đều với vận tốc góc ωω quanh trục thẳng đúng đi qua tâm của đĩa. Trên đĩa có một thanh mảnh đồng chất AB có thể quay tự do quanh trục được gắn chặt với đĩa và đi qua đầu A của thanh. Khi thanh AB đang ở vị trí như hình vẽ, tác động nhẹ vào đầu B của thanh để thanh AB quay với vận tốc góc ban đầu ω0ω0 so với đĩa (ω0ω0khá nhỏ so với ωω). Người ta quan sát đứng trên đĩa sẽ thấy thanh chuyển động như thế nào?