Cho hình vẽ sau:
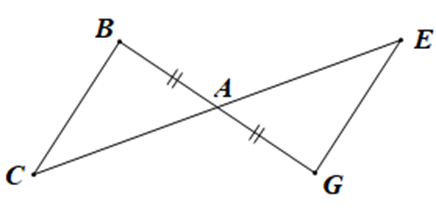
Điều kiện để DABC = DAGE theo trường hợp cạnh – góc – cạnh là:
A. \(\widehat {ACB} = \widehat {AGE};\)
B. AC = EG;
C. AC = AE;
D. BC = AG.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Vì DABC = DAGE theo trường hợp cạnh – góc – cạnh nên điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.
Mà \(\widehat {BAC} = \widehat {GAE}\) (hai góc đối đỉnh)
Góc BAC xen kẽ giữa hai cạnh AB và AC, góc GAE xen kẽ giữa hai cạnh AG và AE.
Mà AB = AG nên điều kiện còn thiếu trong trường hợp này là điều kiện về cạnh, đó là AC = AE.
Vậy ta chọn phương án C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình vuông ABCD, trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N và trên cạnh DC lấy điểm P sao cho AM = BN = CP. Số đo góc MNP là:
Cho tam giác ABC và tam giác DEG có: AB = DE, \(\widehat {ABC} = \widehat {DEG}.\) Điều kiện để DABC = DDEG theo trường hợp cạnh – góc – cạnh là:
Cho tam giác ABC có AB = AC = BC, phân giác BD và CE cắt nhau tại O. Chọn phát biểu sai:
Cho hình vẽ dưới đây:
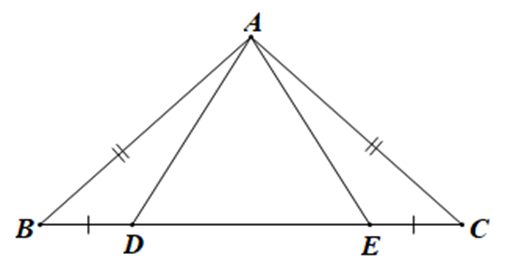
Biết AB = AC, BD = EC, . Xét các khẳng định sau:
(1) DABD = DACE;
(2) DABE = DACD.
Chọn câu đúng:
Cho tam giác BAC và tam giác MNP có BA = MN, CA = MP. Phát biểu nào sau đây là đúng:
Cho góc nhọn xOy và một điểm A nằm trong góc đó. Kẻ AH ^ Ox tại H và AK ^ Oy tại K. Kéo dài AH một đoạn HB = AH và kéo dài AK một đoạn KC = AK. Nối OA, OB, OC. Chọn phát biểu đúng:
Cho hình vẽ dưới đây:
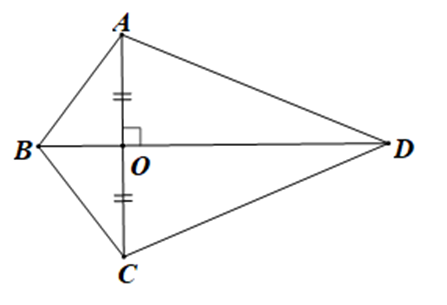
Số cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh là:
Cho DABC và DMNP có AB = NP, \(\widehat B = \widehat N = 55^\circ ,\) BC = NM. Biết \(\widehat A = 50^\circ ,\) số đo góc P là:
Cho góc xOy khác góc bẹt, gọi Ot là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia đối của tia Ot lấy điểm C tuỳ ý. Chọn phát biểu đúng: