Cho DABC = DDEG. Biết \(\widehat A + \widehat B = 140^\circ ,\widehat E = 45^\circ .\) Khẳng định nào sau đây là đúng?
A. \(\widehat A > \widehat B > \widehat C;\)
B. \(\widehat A > \widehat C > \widehat B;\)
C. \(\widehat B > \widehat A > \widehat C;\)
D. \[\widehat C > \widehat B > \widehat A.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right)\)
Hay \(\widehat C = 180^\circ - 140^\circ = 40^\circ \)
Vì DABC = DDEG nên ta có \(\widehat B = \widehat E\) (hai góc tương ứng)
Do đó \(\widehat B = 45^\circ \)
Mà \(\widehat A + \widehat B = 140^\circ \) nên \(\widehat A = 140^\circ - \widehat B = 140^\circ - 45^\circ = 95^\circ \)
Vì 95° > 45° > 40°
Do đó \(\widehat A > \widehat B > \widehat C\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho DABC = DDEG, biết AC = 5 cm. Cạnh nào của tam giác DEG có độ dài bằng 5 cm?
Cho tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng tam giác có ba đỉnh O, H, K. Biết \(\widehat A = \widehat O,\widehat B = \widehat K.\) Kí hiệu về sự bằng nhau của hai tam giác là:
Trong hình vẽ sau:
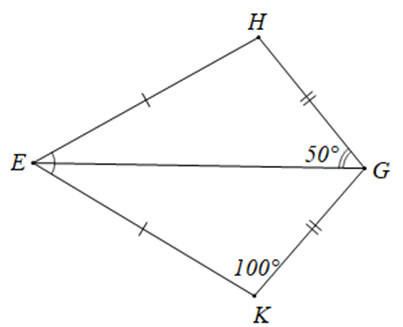
Biết EG là tia phân giác của \(\widehat {HEK}\) và \(\widehat {HEK} = 60^\circ .\) Hãy chọn khẳng định đúng trong các khẳng định sau:
Cho hai tam giác ABC và DEG có: AB = DE, AC = DG, BC = EG, \(\widehat A = \widehat D,\)\(\widehat B = \widehat E,\) \(\widehat C = \widehat G.\) Cách viết nào dưới đây là đúng?
Cho hai tam giác ABC và MNP như hình vẽ dưới đây:
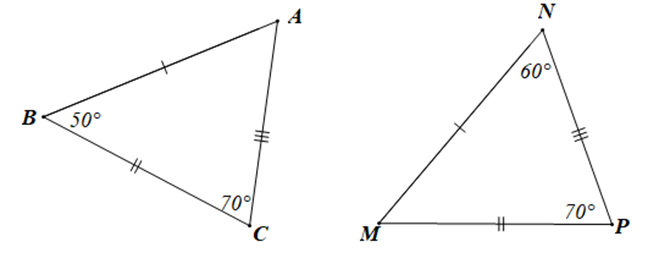
Khẳng định nào sau đây là đúng?
Cho hai tam giác bằng nhau. Tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và tam giác có ba đỉnh là M, N, P. Biết AB = MP, \(\widehat C = \widehat N.\) Khẳng định nào sau đây là đúng nhất?
Cho DABC = DMNP có AB = 2 cm, BC = 3 cm, MP = 4cm. Chu vi tam giác MNP là:
Cho DABC = DMNP biết \(\widehat A = 75^\circ ,\widehat B = 55^\circ .\) Số đo góc P là: