Cho ∆ABC có AI, BH, CK là các đường cao (I ∈ BC, K ∈ AB, H ∈ AC). Biết ∆ABH = ∆ACK. Kết luận nào sau đây đúng?
A. \[\widehat {HBA} \ne \widehat {KCA}\];
B. HB ≠ KC;
C. \[\widehat {ABH} = \widehat {KAC}\];
D. CH = BK.
Giải bởi Vietjack
Đáp án đúng là: D
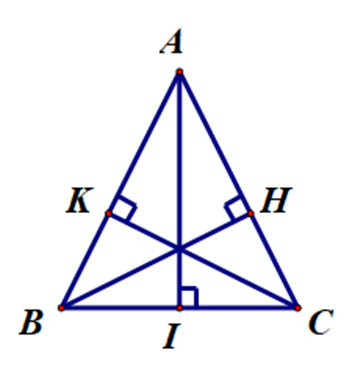
Ta có ∆ABH = ∆ACK (giả thiết).
Ta suy ra \[\widehat {HBA} = \widehat {KCA}\]; HB = KC (cặp góc, cặp cạnh tương ứng).
Do đó đáp án A, B sai.
Ta có: ∆ABH = ∆ACK (giả thiết).
Mà \[\widehat {ABH},\,\,\widehat {KAC}\] không phải cặp góc tương ứng.
Do đó \[\widehat {ABH} \ne \widehat {KAC}\].
Suy ra đáp án C sai.
Ta có: ∆ABH = ∆ACK (giả thiết).
Ta suy ra AH = AK và AB = AC (các cặp góc tương ứng).
Do đó AB – AK = AC – AH.
Suy ra BK = CH (vì K ∈ AB, H ∈ AC).
Do đó đáp án D đúng.
Vậy ta chọn đáp án D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho ∆ABC vuông tại A có AB < AC, \[\widehat B = 60^\circ \]. Kẻ AH ⊥ BC (H ∈ BC). Gọi D là điểm trên cạnh AC sao cho AD = AB. Kẻ DE ⊥ BC (E ∈ BC) và DK ⊥ AH (K ∈ AH). Cho các khẳng định sau:
(I) BH = AK;
(II) HA = KD = HE.
Chọn phương án đúng:
Cho ∆ABC vuông tại A. Trên cạnh BC, lấy điểm D sao cho BD = BA = 5 cm. Đường thẳng vuông góc với BC tại D cắt AC tại H. Gọi E là giao điểm của DH và AB. Biết CD = 3 cm. Độ dài cạnh BE bằng
Cho ∆ABC vuông tại A và ∆MNP vuông tại M có AB = MN, CB = PN. Biết AC = 5 cm. Tính độ dài MP.
Cho ∆ABC vuông tại A, tia phân giác \[\widehat B\] cắt AC tại D. Kẻ DE ⊥ BC tại E. Gọi H là giao điểm của BD và AE. Đường thẳng BH vuông góc với đường thẳng nào trong các đường thẳng sau đây.
Cho ∆ABC nhọn và ∆ABC = ∆DEF. Kẻ AH ⊥ BC (H ∈ BC) và DK ⊥ EF (K ∈ EF). Kết luận nào sau đây là đúng?
Cho ∆ABC có M là trung điểm BC. Kẻ BE và CF lần lượt cùng vuông góc với AM ở E và F. Khi đó ta có BF song song với đường thẳng nào trong các đường thẳng sau đây.
