Cho tam giác ∆HAB cân tại H và I là trung điểm của AB (như hình bên dưới). Góc HIB có số đo là:
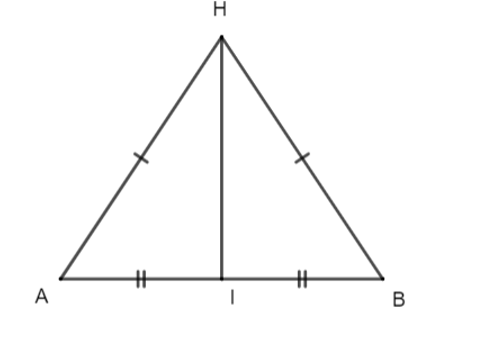
A. 45°;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Xét ∆HIA và ∆HIB có:
AI = IB (I là trung điểm của đoạn thẳng AB);
HA = HB (∆HAB cân tại H);
HI là cạnh chung.
Do đó ∆HIA = ∆HIB (c.c.c)
Suy ra = (hai góc tương ứng).
mà + = 180°.
nên = 180° : 2 = 90°.
Vậy số đo góc = 90°.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
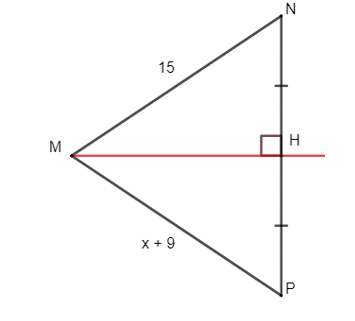
Quan sát hình bên dưới, cho biết MH là đường trung trực của đoạn thẳng NP, cho MN = 15. Vậy x có giá trị là:
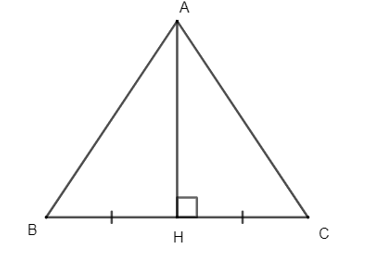
Cho tam giác ABC có AH là đường trung trực của đoạn thẳng BC và H nằm trên đoạn thẳng BC. Cho góc . Tính số đo góc .
Cho ∆ABC có đường trung trực AH với H thuộc đoạn thẳng BC, cho AH = 5 cm, BC = 8 cm. Diện tích tam giác AHC bằng:
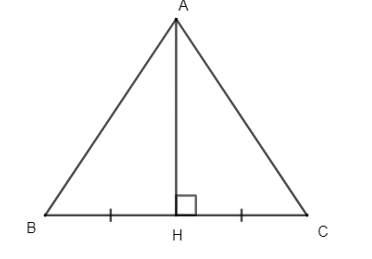
Cho tam giác ABC có AH là đường trung trực của BC và H nằm trên đoạn thẳng BC. Tính số đo góc biết số đo góc .
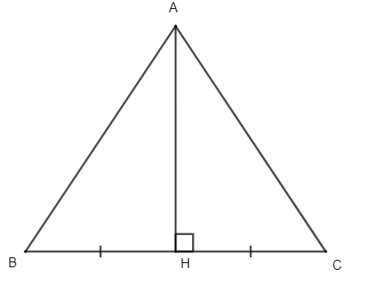
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
Cho tam giác ∆ABC có đường cao AH và H là trung điểm của BC. Vậy tam giác ABC là:
Quan sát hình bên dưới, cho biết H là trung điểm của NP, MH vuông góc với NP tại H và MN = 5 cm. Độ dài của đoạn thẳng MP là:
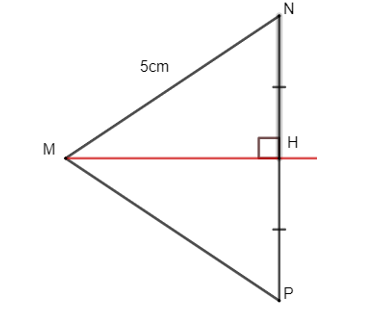
Cho tam giác ABC vuông tại A có = 60°, H là trung điểm của BC. Từ H kẻ đường vuông góc với BC cắt AC tại K. Tính .
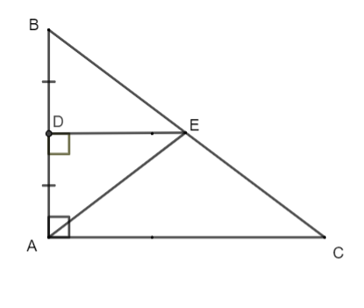
Cho tam giác ABC vuông tại A và D là trung điểm của AB. Từ D kẻ đường thẳng vuông góc với AB cắt BC tại E. Cho AB = 6 cm, AC = 8 cm, DE = 4 cm. Diện tích hình thang DECA là:
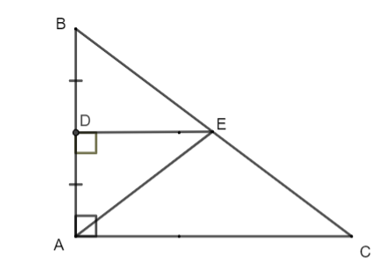
Điền vào chỗ trống sau: “Điểm … hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó”
Cho tam giác ABC vuông tại A và D là trung điểm của AB. Từ D kẻ đường thẳng vuông góc với AB cắt BC tại E.Tính số đo góc biết số đo góc = 30°.
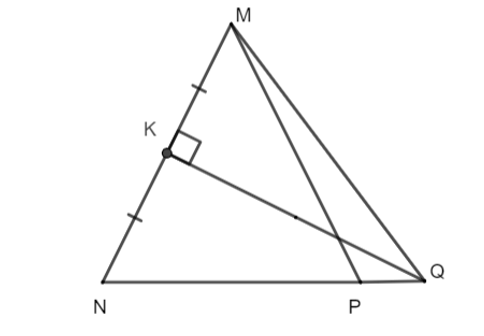
Cho tam giác ΔMNP cân tại M, có , đường trung trực của MN tại trung điểm K của MN cắt NP tại Q. Tính số đo góc .
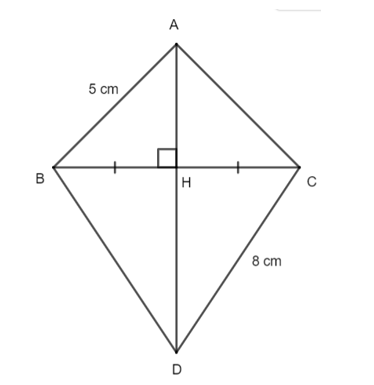
Hình vẽ bên dưới được tạo bởi một đường trung trực qua một đoạn thẳng. Độ dài các cạnh AC và BD là: