\[\widehat {xOy} = 120^\circ \]. Lấy điểm A thuộc tia phân giác của \[\widehat {xOy}\]. Kẻ AB ⊥ Ox tại B, AC ⊥ Oy tại C. Hỏi ∆ABC là tam giác gì?
A. ∆ABC là tam giác cân tại A;
B. ∆ABC là tam giác cân tại B;
C. ∆ABC là tam giác là cân tại C;
D. ∆ABC là tam giác đều.
Giải bởi Vietjack
Đáp án đúng là: D
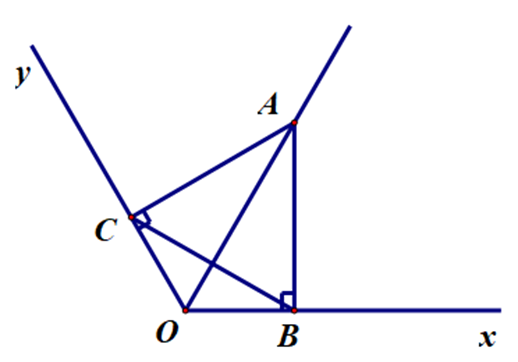
Xét ∆OAB và ∆OAC, có:
\[\widehat {ACO} = \widehat {ABO} = 90^\circ \].
OA là cạnh chung.
\[\widehat {AOC} = \widehat {AOB}\] (OA là phân giác của \[\widehat {xOy}\]).
Do đó ∆OAB = ∆OAC (cạnh huyền – góc nhọn).
Suy ra AB = AC (cặp cạnh tương ứng).
Do đó ∆ABC cân tại A (1).
Ta có OA là phân giác của \[\widehat {xOy}\].
Suy ra \[\widehat {BOA} = \widehat {AOC} = \frac{{120^\circ }}{2} = 60^\circ \].
∆OAB vuông tại B: \[\widehat {BOA} + \widehat {OAB} = 90^\circ \].
Suy ra \[\widehat {OAB} = 90^\circ - \widehat {BOA} = 90^\circ - 60^\circ = 30^\circ \].
Chứng minh tương tự, ta được \[\widehat {OAC} = 30^\circ \].
Do đó ta có \[\widehat {OAB} + \widehat {OAC} = 30^\circ + 30^\circ = 60^\circ \].
Ta suy ra \[\widehat {BAC} = 60^\circ \] (2).
Từ (1), (2), ta suy ra ∆ABC là tam giác đều.
Vậy ta chọn đáp án D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho ∆ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc canh AB sa cho AD = AE. Gọi I là giao điểm của BD và CE. Hỏi ∆IBC là tam giác gì?
Cho ∆ABC đều. Trên các cạnh AB, BC, CA lấy theo thứ tự các điểm D, E, F sao cho AD = BE = CF. Hỏi ∆DEF là tam giác gì?
Cho ∆ABC cân tại A. Trên cạnh BC lấy các điểm M, N sao cho BM = CN. Kết luận nào sau đây là đúng?
Cho ∆ABC vuông tại A (AB < AC). Tia phân giác của \[\widehat A\] cắt BC tại D. Qua D kẻ đường thẳng vuông góc BC, cắt AC tại E. Trên AB lấy điểm F sao cho AF = AE. Hỏi ∆DBF là tam giác gì?
