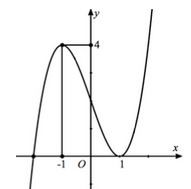
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ bên, một hàm số g(x) xác định theo f(x) có đạo hàm $g\text{'}\left(x\right)=f\left(x\right)+m$ . Tìm tất cả các giá trị thực của tham số mm để hàm số g(x) có duy nhất một cực trị.

Trong không gian Oxyz, cho hai mặt phẳng $\left(\alpha \right):x-my+z+6m+3=0$ và $\left(\beta \right):mx+y-mz+3m-8=0$ ; hai mặt phẳng này cắt nhau theo giao tuyến là đường thẳng $\Delta$. Gọi $\Delta \text{'}$ là hình chiếu của $\Delta$ lên mặt phẳng Oxy. Biết rằng khi mm thay đổi thì đường thẳng $\Delta \text{'}$ luôn tiếp xúc với một mặt cầu cố định có tâm I(a;b;c) thuộc mặt phẳng Oxy. Tính giá trị biểu thức $P=10a^2-b^2+3c^2$.

Trong không gian Oxyz, cho điểm S(−2;1;−2) nằm trên mặt cầu $\left(S\right):x^2+y^2+z^2=9$. Từ điểm S kẻ ba dây cung SA,SB,SC với mặt cầu (S) có độ dài bằng nhau và đôi một tạo với nhau góc 60⁰. Dây cung AB có độ dài bằng:

Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng $\left(P\right):2x+2y-z-3=0$ và mặt cầu $\left(S\right):{\left(x-3\right)}^2+{\left(y-2\right)}^2+{\left(z-5\right)}^2=36$. Gọi $\Delta$ là đường thẳng đi qua E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của $\Delta$ là:

Trong không gian với hệ tọa độ  Oxyz, cho mặt phẳng (P):2x−y−2z+1=0 và ba điểmA(1;−2;0), B(1;0;−1) và C(0;0;−2). Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB,AC,BC?

Trong không gian với hệ tọa độ Oxyz , cho đường thẳng $d:\left\{\begin{array}{c}x=t\\ y=-1\\ z=-t\end{array}\right.$và 2 mặt phẳng (P)  và (Q) lần lượt có phương  trình $x+2y+2z+3=0;x+2y+2z+7=0$. Viết phương trình mặt cầu (S) có tâmI  thuộc đường thẳng d, tiếp xúc với hai mặt phẳng (P)  và (Q).

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình: $x^2+y^2+z^2-2x+4y-2z-3=0$ và đường thẳng $\Delta :\frac{x}{2}=\frac{y+1}{-2}=z$ . Mặt phẳng (P) vuông góc với Δ và tiếp xúc với (S) có phương trình là 

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d:\frac{x-1}{-1}=\frac{y-2}{1}=\frac{z+1}{2}$, điểm A(2;−1;1). Gọi I là hình chiếu vuông góc của A lên d. Viết phương trình mặt cầu (C) có tâm I và đi qua A.

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d:\left\{\begin{array}{c}x=2t\\ y=t\\ z=4\end{array}\right.$ và $d\text{'}:\left\{\begin{array}{c}x=t\text{'}\\ y=3-t\text{'}\\ z=0\end{array}\right.$ . Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng d và d′ là: 

Trong không gian với hệ tọa độ  Oxyz,  cho mặt cầu (S) có phương trình ${\left(x-1\right)}^2+{\left(y+2\right)}^2+{\left(z-3\right)}^2=50$.Trong số các đường thẳng sau, mặt cầu (S) tiếp xúc với đường thẳng nào.