Cho hình nón có góc ở đỉnh bằng 1200 và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
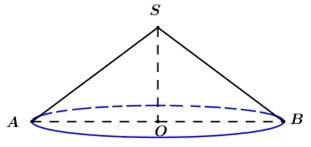
Gọi S là đỉnh hình nón, AB là 1 đường kính của hình nón và O là tâm đường tròn đáy của hình nón.
Khi đó ta có và
Ta có: cân tại S suy ra SO là phân giác của
Xét tam giác vuông SOA có:
Vậy diện tích xung quanh của hình nón là:
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC đều, có diện tích bằng s1 và AH là đường cao. Quay tam giác ABC quanh đường thẳng AH ta thu được hình nón có diện tích xung quanh bằng s2. Tính .
Cho mặt cầu tâm O bán kính R. Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình nón N có đỉnh S nằm trên mặt cầu, có đáy là đường tròn (C) và có chiều cao h (h > R). Tìm hh để thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất.
Một hình nón đỉnh S có bán kính đáy bằng , góc ở đỉnh là 1200. Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất Smax của thiết diện đó là bao nhiêu?
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón bằng:
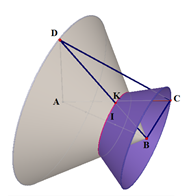
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD,BC; AD = 3BC = 3a, AB = a,. Điểm I thỏa mãn ; M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD).
Công thức tính diện tích toàn phần hình nón có bán kính đáy r, độ dài đường cao h và độ dài đường sinh l là:
Công thức tính thể tích khối nón có bán kính đáy r, độ dài đường sinh l và chiều cao h là:
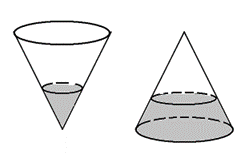
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 10cm. Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?
Cho hình nón N1 có chiều cao bằng 40cm. Người ta cắt hình nón N1 bằng một mặt phẳng song song với đáy của có để được một hình nón nhỏ N2 có thể tích bằng 18 thể tích N1. Tính chiều cao h của hình nón N2?
Cho hình hộp có đáy là hình thoi cạnh a và góc . Mặt chéo ACC′A′ nằm trong mặt phẳng vuông góc với đáy, đồng thời là hình thoi có góc .
Tính thể tích khối tứ diện ACB′D′.
Cho hình nón có các kích thước r = 1cm; l = 2cm với r, l lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:
Cho hình nón có diện tích xung quanh bằng và bán kính đáy bằng a. Tính độ dài đường sinh l của hình nón đã cho.
Cho tam giác ABO vuông tại O, có góc Quay tam giác ABO quanh trục AO ta được một hình nón có diện tích xung quanh bằng:
Một hình nón có bán kính đáy bằng 1, chiều cao nón bằng 2. Khi đó góc ở đỉnh của nón là thỏa mãn