Trong mặt phẳng Oxy cho đường thẳng và đường tròn . Tìm những điểm M thuộc (C) và N thuộc (d) sao cho MN có độ dài nhỏ nhất.
A.
B.
C.
d.
 Giải bởi Vietjack
Giải bởi Vietjack
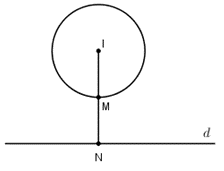
Đường tròn (C) có tâm I(−1;3) và bán kính
Ta có:
Suy ra d không cắt (C).
Ta có
MN min ⇔ IN đạt min ⇔⇔ N là chân hình chiếu vuông góc của I xuống đường thẳng d.
Giả sử .Vì nên ta có
Mặt khác, ta có: IN vuông góc với d nên . Mà
.Suy ra ta có:
Từ (1) và (2) ta có hệ phương trình
Vì nên M là trung điểm của IN. Do đó, tọa độ của M là:
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (m là tham số). Biết đường tròn (Cm)(Cm) có bán kính bằng 5. Khi đó tập hợp tất cả các giá trị của m là
Với điều kiện nào của m thì phương trình sau đây là phương trình đường tròn ?
Phương trình đường tròn (C) đi qua hai điểm A(0;1),B(1;0) và có tâm nằm trên đường thẳng: là:
Phương trình đường tròn (C) có tâm I(2;−4) và đi qua điểm A(1;3) là:
Trong mặt phẳng với hệ trục tọa độ Oxy, cho phương trình đường tròn (m là tham số). Tập hợp các điểm Im là tâm của đường tròn (Cm) khi m thay đổi là:
Trong số các đường tròn có phương trình dưới đây, đường tròn nào đi qua gốc tọa độ O(0,0)?
Phương trình đường tròn (C) đi qua 33 điểm A(0;2),B(−2;0) và C(2;0) là:
Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai đường thẳng và tam giác ABC có A(2;3), trọng tâm là G(2;0), điểm B thuộc d1 và điểm Cthuộc d2. Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Đường tròn tâm I(a;b)) và bán kính R có phương trình được viết lại thành . Khi đó biểu thức nào sau đây đúng?
Tìm tọa độ tâm I của đường tròn đi qua ba điểm A(0;4), B(2;4), C(4;0).