Hai đường thẳng AB và EF cắt nhau tại O. Kẻ tia ON nằm giữa hai tia OB và OE sao cho \(\widehat {{\rm{EON}}} = \widehat {{\rm{NOB}}}\). Gọi OM là tia đối của tia ON. Chọn khẳng định đúng:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
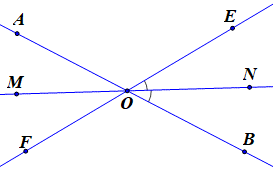
Theo bài ta có \(\widehat {{\rm{EON}}} = \widehat {{\rm{NOB}}}\) (1)
Mà \(\widehat {{\rm{EON}}} + \widehat {{\rm{NOB}}} = \widehat {{\rm{EOB}}}\) (2)
Thay (1) vào (2) ta có: \(\widehat {{\rm{NOB}}} + \widehat {{\rm{NOB}}} = \widehat {{\rm{EOB}}}\)
Hay \(2\widehat {{\rm{NOB}}} = \widehat {{\rm{EOB}}}\)
Suy ra \(\widehat {{\rm{NOB}}} = \frac{1}{2}\widehat {{\rm{EOB}}}\) (3)
Ta lại có hai góc \(\widehat {{\rm{AOM}}}{\rm{ v\`a }}\widehat {{\rm{NOB}}}\) là hai góc ở vị trí đối đỉnh nên:
\(\widehat {{\rm{AOM}}} = \widehat {{\rm{NOB}}}\)(tính chất hai góc đối đỉnh) (4)
Từ (3) và (4) suy ra \(\widehat {{\rm{AOM}}} = \frac{1}{2}\widehat {{\rm{EOB}}}\)
Vậy \(\widehat {{\rm{AOM}}} = \frac{1}{2}\widehat {{\rm{EOB}}}\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho ba đường thẳng xy, zt, mn cắt nhau tại O sao cho \(\widehat {{\rm{zOm}}} = 58^\circ \)và \(\widehat {{\rm{yOt}}} = 35^\circ \) (như hình vẽ).
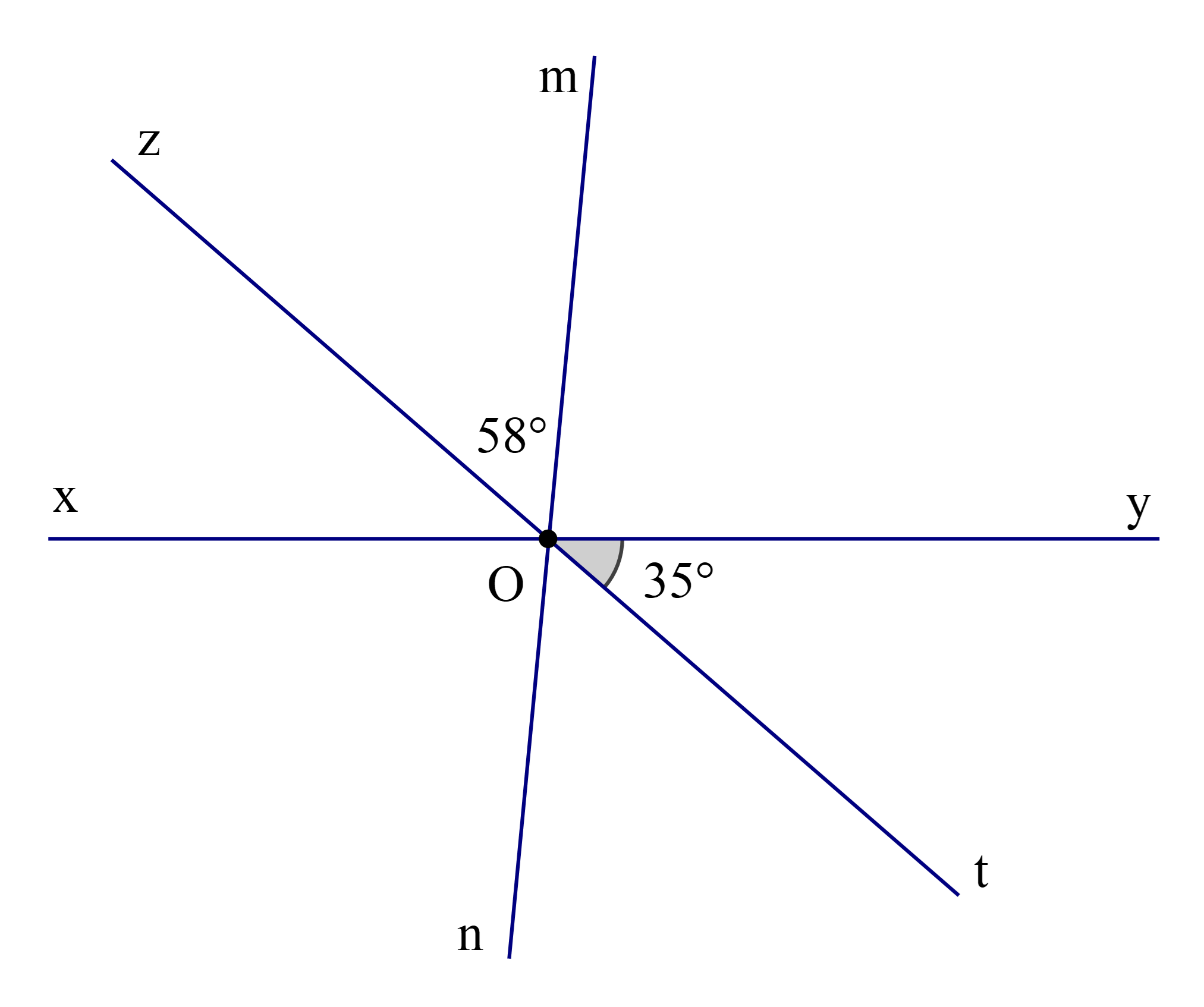
Số đo \(\widehat {{\rm{xOn}}}\) là:
Cho hai góc \(\widehat {\rm{A}}\)và \(\widehat {\rm{B}}\) là hai góc bù nhau, biết rằng \(\widehat {\rm{A}} = 72^\circ \).Chọn khẳng định đúng
Cho ba đường thẳng xy, zt, mn cắt nhau tại O sao \(\widehat {{\rm{nOy}}} = 120^\circ \) và \(\widehat {{\rm{zOm}}} = 2\widehat {{\rm{xOz}}}\). Số đo góc đối đỉnh của \(\widehat {{\rm{zOm}}}\) bằng