Cho a // b, đường thẳng c cắt hai đường thẳng a, b lần lượt tại E và F sao cho \(\widehat {{\rm{MEF}}} = 80^\circ \).
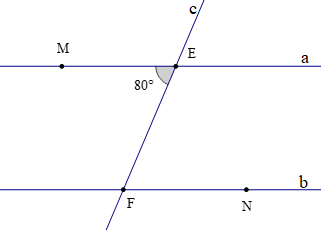
Số đo \(\widehat {EFN}\)là
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
Theo bài ta có a // b mà \(\widehat {{\rm{MEF}}}\) và \(\widehat {EFN}\) là hai góc ở vị trí so le trong.
Do đó \(\widehat {{\rm{MEF}}} = \widehat {EFN}\) (tính chất của hai đường thẳng song song)
Mà \(\widehat {{\rm{MEF}}} = 80^\circ \) nên \(\widehat {EFN} = 80^\circ \)
Vậy ta chọn phương án B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”. Giả thiết của định lí là
Cho \(\widehat {{\rm{DOF}}} = 140^\circ \), biết rằng OE là tia phân giác của \(\widehat {{\rm{DOF}}}\). Số đo của \(\widehat {EOF}\) là
Tia Oz là tia phân giác của \(\widehat {{\rm{xOy}}}\), biết rằng \(\widehat {{\rm{xOz}}} = 40^\circ \). Số đo của \(\widehat {{\rm{yOz}}}\) là:
Quan sát hình vẽ.
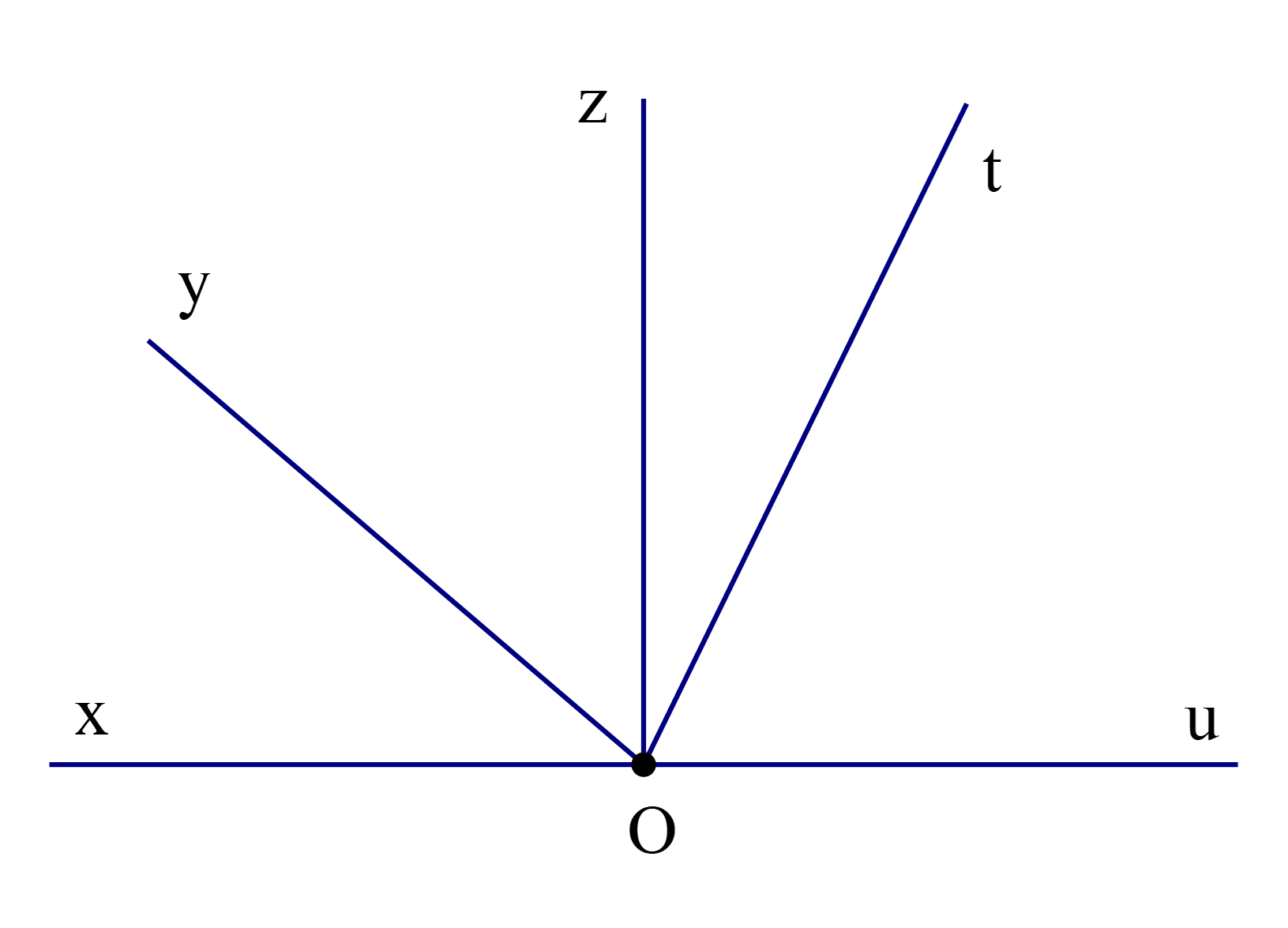
Có tất cả bao nhiêu góc kề (không kể góc bẹt) với \(\widehat {{\rm{xOy}}}\)?
