Cho hình thang ABCD (AB // CD) có AB = BC và \(\widehat {DAC} = 87^\circ ,\widehat {ADC} = 75^\circ \).
Số đo của \(\widehat {{\rm{ACB}}}\) là
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
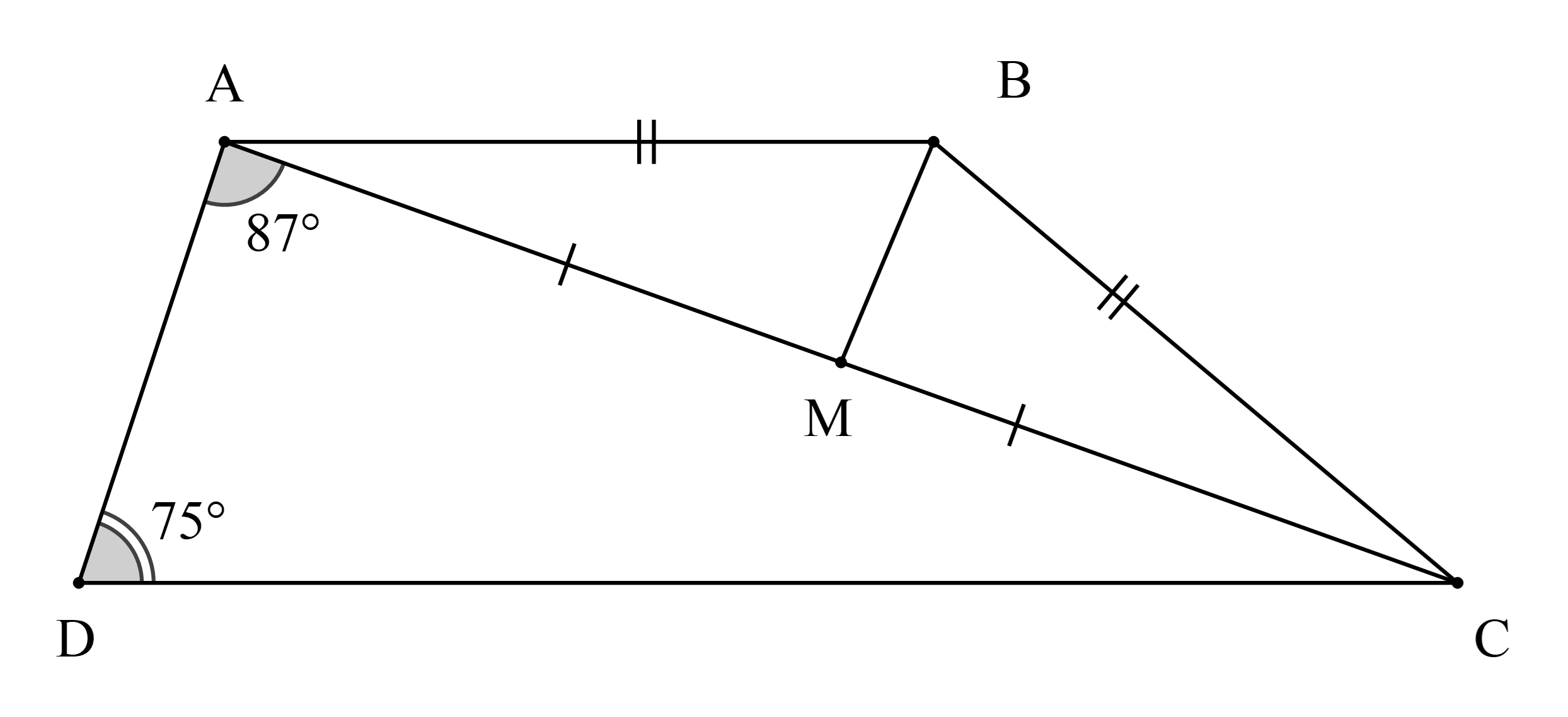
Gọi M là trung điểm của AC.
Xét ∆ADC có \(\widehat {{\rm{DAC}}} + \widehat {\rm{D}} + \widehat {{\rm{ACD}}} = 180^\circ \) (tổng ba góc trong một tam giác bằng 180°)
Hay \(87^\circ + 75^\circ + \widehat {{\rm{ACD}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{ACD}}} = 180^\circ - 87^\circ - 75^\circ = 18^\circ \)
Theo bài AB // CD nên \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}} = 18^\circ \)(hai góc so le trong).
Xét ∆ABM và ∆CBM có:
AB = CB (giả thiết);
BM là cạnh chung;
AM = CM (giả thiết).
Suy ra ∆ABM = ∆CBM (c.c.c)
Suy ra \(\widehat {{\rm{BAM}}} = \widehat {{\rm{BCM}}}\) (hai góc tương ứng)
Hay \(\widehat {{\rm{BAC}}} = \widehat {{\rm{BCA}}} = 18^\circ \)
Vậy ta chọn phương án B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình thang cân ABCD và ABKH là hình chữ nhật như hình vẽ.
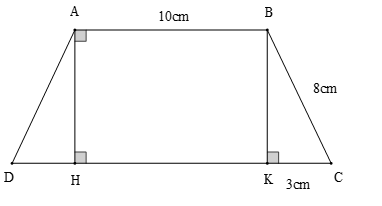
Chu vi tứ giác ABCD là
