Trắc nghiệm Toán 7 CTST Bài 2. Tam giác bằng nhau có đáp án (Phần 2) (Vận dụng)
-
857 lượt thi
-
3 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình thang ABCD (AB // CD) có AB = BC và \(\widehat {DAC} = 87^\circ ,\widehat {ADC} = 75^\circ \).
Số đo của \(\widehat {{\rm{ACB}}}\) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
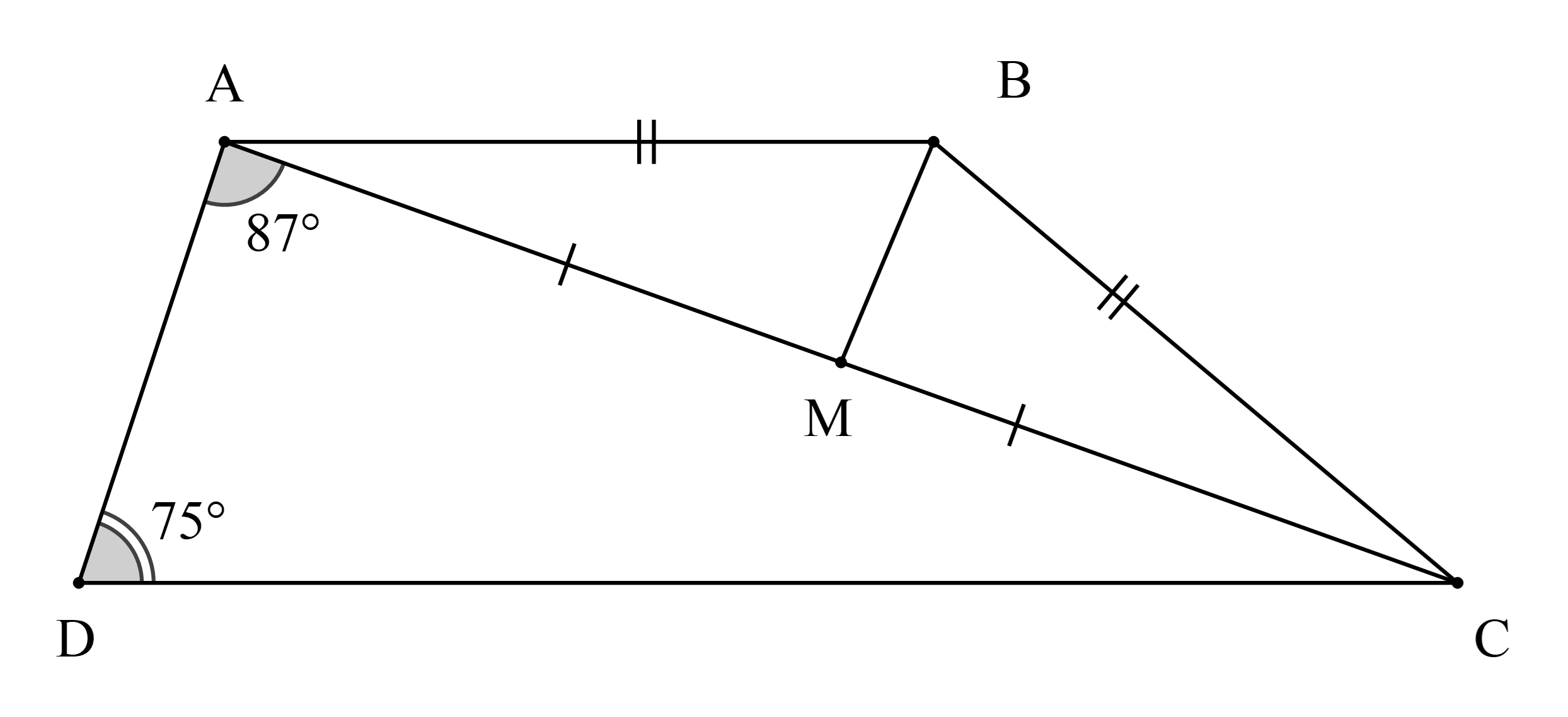
Gọi M là trung điểm của AC.
Xét ∆ADC có \(\widehat {{\rm{DAC}}} + \widehat {\rm{D}} + \widehat {{\rm{ACD}}} = 180^\circ \) (tổng ba góc trong một tam giác bằng 180°)
Hay \(87^\circ + 75^\circ + \widehat {{\rm{ACD}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{ACD}}} = 180^\circ - 87^\circ - 75^\circ = 18^\circ \)
Theo bài AB // CD nên \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}} = 18^\circ \)(hai góc so le trong).
Xét ∆ABM và ∆CBM có:
AB = CB (giả thiết);
BM là cạnh chung;
AM = CM (giả thiết).
Suy ra ∆ABM = ∆CBM (c.c.c)
Suy ra \(\widehat {{\rm{BAM}}} = \widehat {{\rm{BCM}}}\) (hai góc tương ứng)
Hay \(\widehat {{\rm{BAC}}} = \widehat {{\rm{BCA}}} = 18^\circ \)
Vậy ta chọn phương án B.
Câu 2:
Cho hình thang cân ABCD và ABKH là hình chữ nhật như hình vẽ.
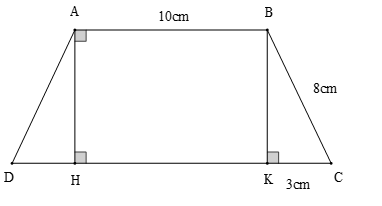
Chu vi tứ giác ABCD là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Do ABCD là hình thang cân nên AD = BC = 8 cm.
Theo bài ABKH là hình chữ nhật
Suy ra AH = BK; AB = HK = 10 cm.
Xét ∆AHD và ∆BKC ta có:
AD = BC (chứng minh trên);
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{BKC}}} = 90^\circ \) (giả thiết);
AH = BK (chứng minh trên).
Suy ra ∆AHD = ∆BKC (cạnh huyền – cạnh góc vuông)
Suy ra DH = CK = 3 cm (hai cạnh tương ứng).
Ta có DC = DH + HK + KC = 3 + 10 + 3 = 16 cm.
Chu vi tứ giác ABCD là:
AB + BC + CD +DA = 10 + 8 + 16 + 8 = 42 (cm).
Vậy ta chọn phương án A.
Câu 3:
Cho hình vẽ

Số đo của \(\widehat {\rm{D}}\) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆AHB và ∆AHC có:
AB = AC (giả thiết);
AH là cạnh chung;
HB = HC (giả thiết).
Suy ra ∆AHB = ∆AHC (c.c.c)
Suy ra \(\widehat {{\rm{ACH}}} = \widehat {{\rm{ABH}}} = (3x + 9)^\circ \)(hai góc tương ứng)
Ta có \(\widehat {{\rm{ACH}}} + \widehat {{\rm{ACD}}} = 180^\circ \)(hai góc kề nhau)
Hay \((3x + 9)^\circ + (9x - 33)^\circ = 180^\circ \)
\((3x + 9 + 9x - 33)^\circ = 180^\circ \)
Suy ra 3x + 9 + 9x −33 = 180
12x – 24 = 180
12x = 180 + 24 = 204
x = 17
Do đó \(\widehat {{\rm{ACD}}} = (9.17 - 33)^\circ = 120^\circ \)
Xét ∆ACD có: \(\widehat {{\rm{DAC}}} + \widehat {{\rm{ACD}}} + \widehat {\rm{D}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(30^\circ + 120^\circ + \widehat {\rm{D}} = 180^\circ \)
Suy ra \(\widehat {\rm{D}} = 180^\circ - 120^\circ - 30^\circ = 30^\circ \)
Vậy ta chọn phương án C.
