Cho ΔABC có góc A bằng 100°. Các đường trung trực của AB và AC cắt cạnh BC theo thứ tự tại E và F. Số đo góc EAF là:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
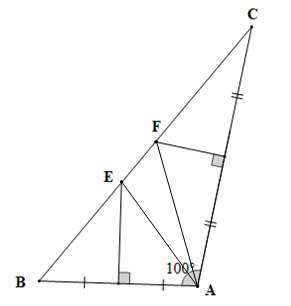
Vì E thuộc đường trung trực của AB nên EA = EB
Do đó tam giác ABE cân tại E
Suy ra \(\widehat B = \widehat {{\rm{BAE}}}\)
Vì F thuộc đường trung trực của AC nên FA = FC
Do đó tam giác ACF cân tại F
Suy ra \(\widehat C = \widehat {{\rm{FAC}}}\)
Xét DABC có \(\widehat B + \widehat {{\rm{CAB}}} + \widehat C = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat B + \widehat C = 180^\circ - \widehat {{\rm{CAB}}} = 180^\circ - 100^\circ = 80^\circ \)
Ta có \(\widehat {{\rm{CAB}}} = \widehat {BA{\rm{E}}} + \widehat {EAF} + \widehat {FAC}\)
Mà \(\widehat B = \widehat {{\rm{BAE}}}\),\(\widehat C = \widehat {{\rm{FAC}}}\),\(\widehat {CAB} = 100^\circ \)
Suy ra \(\widehat {FA{\rm{E}}} = \widehat {{\rm{CAB}}} - \widehat B - \widehat C = 100^\circ - 80^\circ = 20^\circ \).
Vậy ta chọn phương án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC nhọn. Các đường trung trực của AB và AC cắt nhau tại O. Trên tia đối của tia OB lấy điểm D sao cho OB = OD. Biết \(\widehat {ABC} = 75^\circ \), số đó góc ADC là:
Cho tam giác ABC có \(\widehat A = \alpha \) là góc tù. Các đường trung trực của các cạnh AB và AC cắt nhau tại I. Tính số đo của góc BIC theo α ta được: