Cho đường tròn (O) và một dây AB. Vẽ đường kính (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm M. Các đường thẳng CM và DM cắt đường thẳng AB lần lượt tại E và F. Tiếp tuyến của đường tròn tại M cắt đường thẳng AB tại N. Chứng minh rằng N là trung điểm của EF.
Giải bởi Vietjack
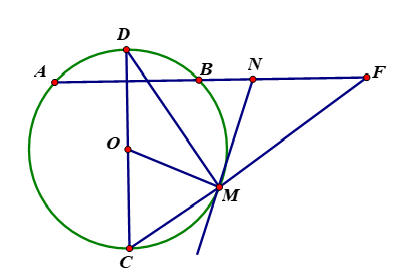
Ta sẽ chứng minh NE = NF bằng cách dùng NM làm trung gian.
Ta có nên và (định lí đường kính vuông góc với dây cung).
Góc F1 là góc có đỉnh ở bên trong một đường tròn nên:
Từ (1) và (2) suy ra do đó cân tại N, suy ra NF = NM.
Góc E là góc có đỉnh ở bên ngoài đường tròn nên: (3)
Góc M2 là góc tạo bởi tia tiếp tuyến và dây cung nên . (4)
Từ (3) và (4) suy ra , dẫn tới (vì )
Do đó cân, suy ra NE = NM tại N. Do vậy NE = NF. Vậy N là trung điểm của EFGói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn (O), hai đường kính AB và CD vuông góc với nhau, điểm M thuộc cung nhỏ BC. Gọi E là giao điểm của MA và CD, F là giao điểm của MD và AB. Chứng minh rằng:
a)
Cho đường tròn (O) và dây AB. Gọi M là điểm chính giữa của cung nhỏ AB và C là điểm nằm giữa A và B. Tia MC cắt đường tròn tại một điểm thứ hai là D.
a) Chứng minh rằng MA2 = MC . MD.
Cho đường tròn (O) và dây AB. Vẽ tiếp tuyến xy // AB có M là tiếp điểm. Chứng minh rằng là tam giác cân.
Cho tứ giác ABCD có bốn đỉnh thuộc đường tròn . Gọi M, N, P, Q lần lượt là điểm chính giữa các cung AB, BC, CD, DA. Chứng minh rằng : .
Cho đường tròn (O) trong đó có ba dây bằng nhau AB, AC, BD sao cho hai dây AC, BD cắt nhau tại M tạo thành góc vuông AMB. Tính số đo các cung nhỏ AB, CD.
b) Khi M di động trên cung nhỏ BC thì diện tích tứ giác AEFD không đổi.
c) Vẽ đường kính MN của đường tròn (O). Chứng minh ba điểm A, O’, N thẳng hàng.
Cho đường tròn (O) và hai đường kính vuông góc AB và CD. Trên cung BD lấy một điểm M. Tiếp tuyến của (O) tại M cắt AB ở E ; CM cắt AB tại F. Chứng tỏ EF = EM.
Cho tam giác ABC, phân giác trong AD. Đường tròn (O) đi qua A, tiếp xúc với BC tại D. Đường tròn (O) cắt AB, AC tương ứng tại M và N. Chứng minh MN // BC.
b) Vẽ đường tròn (O’) ngoại tiếp tam giác ACD. Chứng minh rằng AM là tiếp tuyến của đường tròn (O’).
Cho hình vẽ, hãy điền dấu (x) vào ô thích hợp trong bảng sau:
|
 |
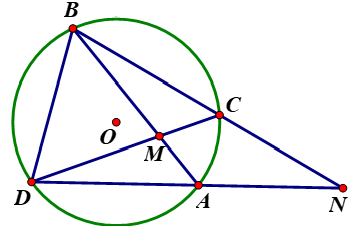Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Vẽ dây AC của đường tròn (O) tiếp xúc với đường tròn (O’). Vẽ dây AD của đường tròn (O’) tiếp xúc với đường tròn (O). Chứng minh rằng:
