Cho tam giác ABC vuông tại A có AM ⊥ BC tại M và M là trung điểm của BC. Gọi D là trung điểm của AC. Từ A kẻ đường thẳng vuông góc với BD tại E. Từ C dựng đường thẳng vuông góc với AC, cắt AE tại G. Biết AB = 2GC. Nhận định nào dưới đây đúng?
A. BD = AG;
B. BD > AG;
C. BD < AG;
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
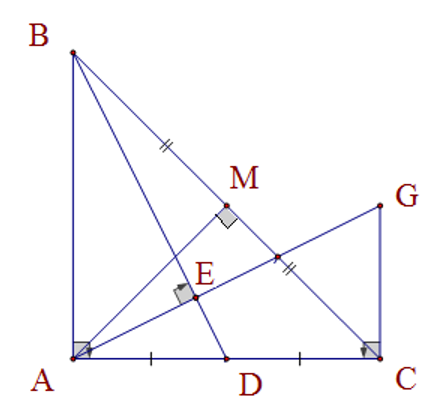
Xét hai tam giác vuông AMB và AMC có:
AM là cạnh chung
MB = MC (giả thiết)
Suy ra ∆AMB = ∆AMC (hai cạnh góc vuông)
Do đó AB = AC (hai cạnh tương ứng)
Có AB = 2GC (giả thiết) suy ra GC =
Mà D là trung điểm của AC nên AD =
Do đó: GC = AD
Xét hai tam giác vuông BAD và ACG có:
BA = AC (chứng minh trên)
AD = CG (chứng minh trên)
Suy ra ∆BAD = ∆ACG (hai cạnh góc vuông)
Do đó BD = AG (hai cạnh tương ứng).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC và BA = BE. Số đo góc BED là
Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. Khẳng định sai là
