Cho ∆ABC cân tại A. Tia phân giác $\widehat{BAC}$ cắt BC tại M. Đường thẳng qua M và vuông góc với AB cắt AB tại H. Đường thẳng qua M và vuông góc với AC cắt AC tại K.

Nhận định nào dưới đây sai?

Hướng dẫn giải

Đáp án đúng là: D

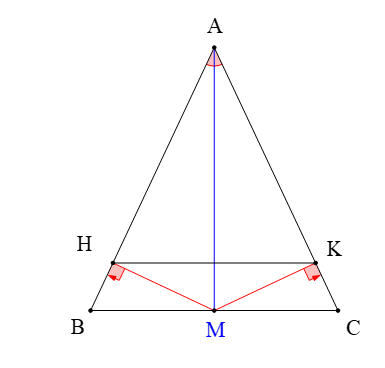
Ta có ∆ABC cân tại A (giả thiết) suy ra AB = AC; $\widehat{B}=\widehat{C}$ (tính chất)

Xét ∆AMB và ∆AMC có:

$\widehat{B}=\widehat{C}$

AB = AC

$\widehat{BAM}=\widehat{CAM}$ (vì AM là tia phân giác góc BAC)

Suy ra ∆AMB = ∆AMC (g.c.g)

Do đó: BM = MC (hai cạnh tương ứng) suy ra M là trung điểm của BC

Xét hai tam giác vuông AMH và AMK có:

AM là cạnh chung

$\widehat{BAM}=\widehat{CAM}$

Suy ra ∆AMH = ∆AMK (cạnh huyền – góc nhọn)

Do đó: AH = AK (hai cạnh tương ứng) suy ra ∆AHK cân tại A

⇒ $\widehat{AHK}=\widehat{AKH}$ (tính chất)

Mà $\widehat{AHK}+\widehat{AKH}+\widehat{BAC}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{AHK}=\frac{180°-\widehat{BAC}}{2}$ (1)

Có $\widehat{B}=\widehat{C}$ mà $\widehat{B}+\widehat{C}+\widehat{BAC}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{B}=\frac{180°-\widehat{BAC}}{2}$ (1)

Từ (1) và (2) suy ra $\widehat{AHK}=\widehat{B}$ mà hai góc đồng vị nên HK // BC.

Vì ∆AMH = ∆AMK (chứng minh trên)

$\widehat{HMA}=\widehat{KMA}$ (hai góc tương ứng) suy ra MA là tia phân giác của góc HMK.

Vậy MA là tia phân giác của góc HMC là sai.