Cho ∆ABC cân tại A. Trên 2 cạnh AB và AC lấy hai điểm M và N sao cho AM = AN. So sánh BN với BC + MN đúng là
A. ;
B. ;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
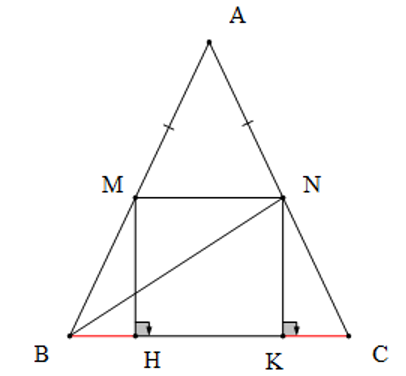
∆ABC cân tại A nên AB = AC và (tính chất)
Mà AM = AN (giả thiết) suy ra BM = CN
Xét hai tam giác vuông MBH và NCK có:
BM = CN
Suy ra ∆MBH = ∆NCK (cạnh huyền – góc nhọn)
Do đó: BH = CK và MH = NK
Có AM = AN (giả thiết) suy ra ∆AMN cân tại A
⇒ (tính chất)
Mà (tổng ba góc của một tam giác)
Suy ra (1)
Có mà (tổng ba góc của một tam giác)
Suy ra (1)
Từ (1) và (2) suy ra mà hai góc đồng vị nên MN // BC.
Mà BC ⊥ MH nên MN ⊥ MH
Xét hai tam giác vuông HMN và NKH có
MH = NK (chứng minh trên)
NH là cạnh chung
Suy ra ∆HMN = ∆NKH (cạnh huyền – cạnh góc vuông)
Do đó MN = HK
Mặt khác: BN > BK (quan hệ đường vuông góc – đường xiên)
Suy ra: 2BN > 2BK = 2(BH + HK) = 2BH + 2HK = BH + KC + MN + HK = BC + MN
Do đó: .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho ∆ABC vuông tại A, M là trung điểm của AB. Vẽ AI ⊥ MC tại I, BK ⊥ MC tại K. So sánh nào dưới đây đúng
Một chiếc thang dài 4 mét được đặt dựa vào tường nhà cao tầng (hình vẽ). Một người thợ sử dụng thang này để đứng lên cao. Trên chiếc thang này người thợ không thể đứng được ở độ cao nào dưới đây?
