Giải bởi Vietjack
Lời giải
Tại x = 0: 4.02 + 3.0 – 1 = – 1;
Tại x = – 1: 4.(– 1)2 + 3.( – 1) – 1 = 0;
Tại x = \[ - \frac{1}{2}\]: \[4.{\left( { - \frac{1}{2}} \right)^2} + 3.\left( { - \frac{1}{2}} \right) - 1 = - \frac{3}{2}\] .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Viết biểu thức đại số biểu thị:
a) Quãng đường đi được sau x(h) của một tàu buýt sông với vận tốc 30 km/h (khi nước yên lặng).
b) Số tiền để mua 25 gói kẹo, biết mỗi gói có giá là x (nghìn đồng).
Biểu thức nào sau đây biểu thị công thức tính chu vi (C) của một hình chữ nhật có độ dài hai cạnh là a và b:
A. C = a.b;
B. \[{\rm{C = }}\frac{{\rm{a}}}{{\rm{b}}}\];
C. C = a2.b;
D. C = 2.(a + b).
Tìm giá trị của x để các biểu thức sau có giá trị bằng 0:
A = 9x + 45;
B = 2x2 – 72.
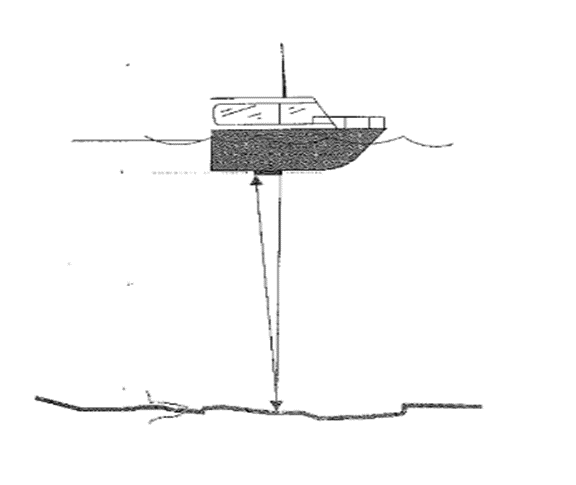
Hiện nay, người ta sử dụng sóng siêu âm để xác định khoảng cách hay đo độ sâu. Khoảng cách đo được là khoảng cách từ bộ phận phát ra tín hiệu tới bề mặt phẳng. Đầu tiên thiết bị đo độ sâu sẽ phát sóng siêu âm vào nước, sau đó thu nhận tín hiệu phản xạ từ đáy nước, từ đó xác định được độ sâu.
a) Một tàu phát ra sóng siêu âm với vận tốc v và thu được âm phản xạ của nó từ đáy biển sau t giây. Viết biểu thức đại số tính khoảng cách S từ tàu đến đáy nước.
Viết biểu thức đại số để diễn đạt các nội dung bên dưới:
a) Tổng của bình phương số a và lập phương số b;
b) Hiệu của 2 lần số a và 5 lần số b;
c) Lập phương của tổng a và b.
Tính giá trị của biểu thức sau tại các giá trị đã cho tương ứng:
Có bao nhiêu biểu thức số, biểu thức đại số trong các biểu thức sau đây: 2x – y; 5.3 – 25; 6.23 + 15; x2y – 5x; x + 2y?
A. Có 1 biểu thức số và 4 biểu thức đại số;
B. Có 3 biểu thức số và 2 biểu thức đại số;
C. Có 2 biểu thức số và 3 biểu thức đại số;
D. Không có biểu thức số và có 5 biểu thức đại số.
Một hình thoi có độ dài hai đường chéo lần lượt là a và b. Lập biểu thức đại số tính diện tích của hình thoi trên theo a và b.
A. S = a.b;
B. S = 2.(a + b);
C. S = \[\frac{1}{2}\]a.b;
D. S = (a.b)2.
Biểu thức đại số biểu thị: “Quãng đường đi được (S) của một xe gắn máy trong thời gian (t) với vận tốc 45 km/h là:
A. S = \[\frac{{45}}{t}\];
B. S = 45.t;
C. \[{\rm{S = }}\frac{{\rm{t}}}{{{\rm{45}}}}\];
D. \[{\rm{t = }}\frac{{{\rm{45}}}}{{\rm{S}}}\].
