Tìm các số x không âm thỏa mãn
A.
B. x < 9
C. x > 9
D.
 Giải bởi Vietjack
Giải bởi Vietjack
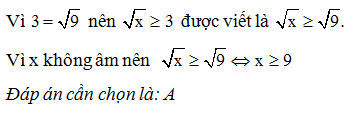
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
1. Căn bậc hai
a. Khái niệm: Căn bậc hai của một số a không âm là số x sao cho
Ví dụ 1. Số 16 là số không âm, căn bậc hai của 16 là số x sao cho
Do đó căn bậc hai của 16 là 4 và −4.
b. Tính chất:
- Số âm không có căn bậc hai.
- Số 0 có đúng một căn bậc hai đó chính là số 0, ta viết .
- Số dương a có đúng hai căn bậc hai là hai số đối nhau; số dương ký hiệu là , số âm ký hiệu là .
Ví dụ 2.
- Số −12 là số âm nên không có căn bậc hai.
- Số 64 có hai căn bậc hai là 8 và −8.
- Số 15 có hai căn bậc hai là và .
2. Căn bậc hai số học
a. Định nghĩa: Với số dương a, số được gọi là căn bậc hai số học của a. Số 0 cũng được gọi là căn bậc hai số học của 0.
Ví dụ 3. Căn bậc hai số học của 36 là (= 6).
- Căn bậc hai số học của 7 là .
Chú ý. Với a ≥ 0, ta có:
Nếu thì x ≥ 0 và
Nếu x ≥ 0 và thì .
- Ta viết
Ví dụ 4. Tìm căn bậc hai số học của các số sau đây: 25; 81; 225; 324.
Lời giải:
Ta có:
• vì 5 > 0 và
• vì 9 > 0 và
• vì 15 > 0 và ;
• vì 18 > 0 và
b. Phép khai phương:
- Phép khai phương là phép toán tìm căn bậc hai số học của số không âm (gọi tắt là khai phương).
- Khi biết một căn bậc hai số học của một số, ta dễ dàng xác định được các căn bậc hai của nó.
Ví dụ 5.
- Căn bậc hai số học của 9 là 3 nên 9 có hai căn bậc hai là 3 và −3.
- Căn bậc hai số học cuả 256 là 16 nên 256 có hai căn bậc hai là 16 và −16.
3. So sánh các căn bậc hai số học
Định lí. Với hai số a và b không âm, ta có: .
Ví dụ 6. So sánh:
a) 3 và ;
b) 5 và .
Lời giải:
a) Vì 9 < 11 nên .
Vậy .
b) Vì 25 > 15 nên .
Vậy .