Trong các điểm: A (1; 2); B (−1; −1); C (10; −200); D có bao nhiêu điểm thuộc đồ thị hàm số (P): y = -
A. 1
B. 4
C. 3
D. 2
 Giải bởi Vietjack
Giải bởi Vietjack
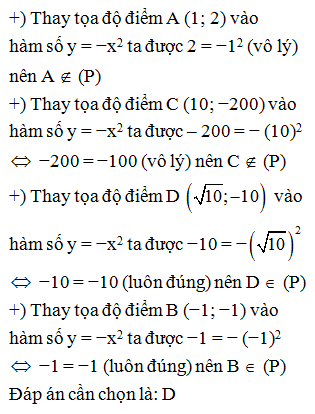
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số y = f(x) = (−2m + 1)x2. Tìm giá trị của m để đồ thị đi qua điểm A (−2; 4)
Cho hàm số y = (4 – 3m)x2 với m . Tìm m để hàm số đồng biến với mọi x < 0
Cho hàm số x2 với 7. Tìm m để hàm số nghịch biến với mọi x < 0.
Cho hàm số y = f(x) x2. Tổng các giá trị của a thỏa mãn f(a) = 3 +
Cho hàm số y = f(x) = −2x2. Tổng các giá trị của a thỏa mãn f(a) = −8 + 4
Cho hàm số y = f(x) x2. Tìm giá trị của m để đồ thị đi qua điểm B (−3; 5)
1. Định nghĩa hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số cho trước và a ≠ 0.
Chú ý: Khi b = 0 ta có hàm số y = ax (đã học ở lớp 7)
Ví dụ 1. Cho các hàm số:
y = 3x; y = x + 2; ;
y = 3x + 1; y = 4x − 1; y = 2 − 3x;
Đây là các hàm số bậc nhất.
2. Tính chất hàm số bậc nhất
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có các tính chất như sau:
• Đồng biến trên R khi a > 0.
• Nghịch biến trên R khi a < 0.
Ví dụ 2. Cho các hàm số sau: y = 4x – 1, y = − 2x + 1, ; . Hàm số nào đồng biến, hàm số nào nghịch biến?
Lời giải:
- Hàm số y = 4x – 1 có a = 4 > 0 nên hàm số này đồng biến trên R.
- Hàm số y = − 2x + 1 có a = − 2 < 0 nên hàm số này nghịch biến trên R.
- Hàm số có > 0 nên hàm số này đồng biến trên R.
- Hàm số có < 0 nên hàm số này nghịch biến trên R.
Vậy hàm số đồng biến là: y = 4x – 1; ;
Hàm số nghịch biến là: y = − 2x + 1; .