Một vật dao động điều hòa theo phương trình (t tính bằng giây). Tìm quãng đường vật đi được kể từ lúc bắt đầu dao động đến li độ x = - 2cm theo chiều âm lần thứ nhất?
A.
B.
C.
D. 16cm
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Tại t = 0
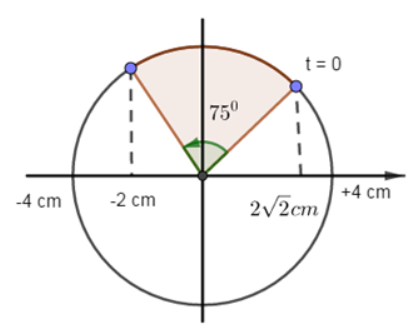
=> Quãng đường vật đi được:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho một chất điểm dao động điều hòa với tần số 1Hz, thời điểm đầu vật qua vị trí x = 5cm theo chiều dương với tốc độ v=10πcm/s. Viết phương trình dao động.
Một vật dao động điều hoà có đồ thị như hình vẽ.
Phương trình dao động của vật là:
Một vật dao động điều hòa với biên độ A. Quãng đường lớn nhất vật đi được trong khoảng thời gian là:
Một vật dao động điều hòa có vận tốc cực đại là và gia tốc cực đại là . Chu kì dao động của vật là:
Một vật dao động điều hòa có chu dao động T = 2s, vận tốc cực đại mà vật đạt được có giá trị . Biết tại thời điểm ban đầu, vận tốc của vật bằng 0 và đang đi theo chiều âm. Phương trình dao động của vật là:
Một vật dao động điều hòa theo phương trình . Kể từ thời điểm t = 0, sau thời gian bao lâu thì vật đi được quãng đường 7,5 cm.
Một vật dao động điều hòa có đồ thị li độ theo thời gian như hình vẽ:
Pha ban đầu của dao động bằng:
Một vật dao động điều hòa dọc theo trục Ox với tần số góc ω = 10 rad/s. Tại thời điểm t, vận tốc và gia tốc của vật lần lượt là 20cm/s và . Tốc độ dao động cực đại của vật là:
Một chất điểm dao động điều hòa với chu kì T. Trong khoảng thời gian ngắn nhất khi đi từ vị trí có li độ đến vị trí , chất điểm có tốc độ
Một vật dao động điều hòa từ A đến B với chu kỳ T, vị trí cân bằng O. Trung điểm OA, OB là M, N. Thời gian ngắn nhất để vật đi từ M đến N là . Hãy xác định chu kỳ dao động của vật.
Vật dao động điều hoà theo phương trình cm. Quãng đường vật đi được trong khoảng thời gian từ đến là:
Một vật dao động điều hòa theo phương trình (t tính bằng giây). Tìm quãng đường vật đi được kể từ lúc bắt đầu dao động đến khi vật có tốc độ lần thứ hai?
Một chất điểm dao động điều hòa có chu kì T. Trong khoảng thời gian ngắn nhất khi tốc độ của vật tăng từ 0 đến giá trị thì chất điểm có tốc độ trung bình là
Một vật dao động điều hòa theo phương trình . Xác định thời gian vật chuyển động từ thời điểm t=0,75s đến khi vật có li độ lần thứ 2?
I. Dao động cơ
1. Thế nào là dao động cơ?
- Dao động cơ học là dạng chuyển động qua lại quanh một vị trí đặc biệt gọi là vị trí cân bằng.
- Vị trí cân bằng là vị trí mà chất điểm không chịu lực tác dụng hoặc hợp lực tác dụng lên chất điểm bằng không.
2. Dao động tuần hoàn
Dao động tuần hoàn là dao động mà trạng thái của vật được lặp lại như cũ, theo hướng cũ sau những khoảng thời gian bằng nhau xác định.
II. Phương trình của dao động điều hòa
- Dao động điều hòa là dao động mà li độ của vật là một hàm cosin hay (sin) của thời gian.
- Phương trình dao động
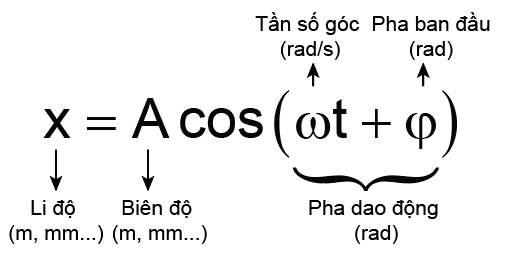
Trong đó:
+ A: là biên độ dao động, hay độ lệch cực đại của vật, vì thế biên độ dao động là một số dương.
+ (): là pha của dao động tại thời điểm t. Với một biên độ đã cho thì pha là đại lượng xác định vị trí và chiều chuyển động của vật tại thời điểm t.
+ : là pha ban đầu của dao động cho phép xác định vị trí và chiều chuyển động của vật tại thời điểm ban đầu, có giá trị nằm trong khoảng từ đến .
- Chú ý: Pha ban đầu theo các vị trí đặc biệt
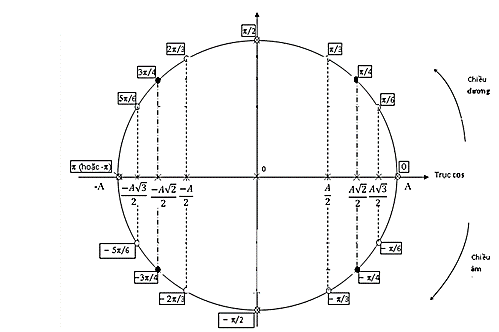
III. Chu kì. Tần số. Tần số góc của dao động điều hòa
1. Chu kì và tần số
- Chu kì dao động (T) là khoảng thời gian ngắn nhất để vật thực hiện một dao động toàn phần. Đơn vị của chu kì là giây (s).
Trong đó N là số dao động toàn phần chất điểm thực hiện được trong khoảng thời gian t.
- Tần số dao động (f) là số dao động toàn phần vật thực hiện được trong một giây. Đơn vị của tần số là Héc (Hz)
2. Tần số góc
Là đại lượng liên hệ với chu kì T hay tần số f bằng hệ thức:
(rad/s)
IV. Vận tốc và gia tốc của vật dao động điều hòa
1. Vận tốc
- Vận tốc là đạo hàm của li độ theo thời gian:
+ Khi vật đi từ - A đến A thì vận tốc có giá trị dương, vận tốc có giá trị cực đại khi vật đi qua vị trí cân bằng
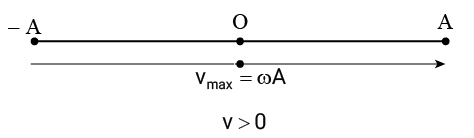
+ Khi vật đi từ A đến –A thì vận tốc có giá trị âm, vận tốc có giá trị cực tiểu khi vật đi qua vị trí cân bằng
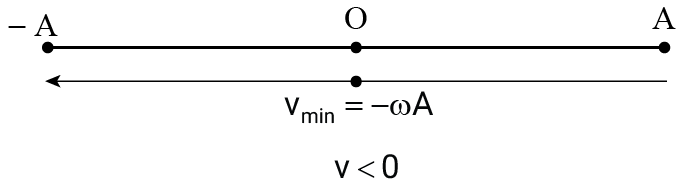
- Tốc độ là độ lớn vận tốc:
+ Tại vị trí biên x = : tốc độ cực tiểu:
+ Tại VTCB x = 0: tốc độ cực đại: .
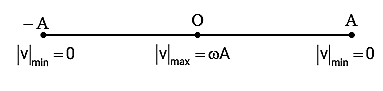
2. Gia tốc
- Gia tốc là đạo hàm của vận tốc theo thời gian:
Vec tơ gia tốc luôn hướng về vị trí cân bằng và có độ lớn tỉ lệ với độ lớn của li độ.
+ Gia tốc cực đại tại vị trí biên âm:
+ Gia tốc cực tiểu tại vị biên dương:
+ Gia tốc bằng 0 tại vị trí cân bằng

V. Đồ thị của dao động điều hòa
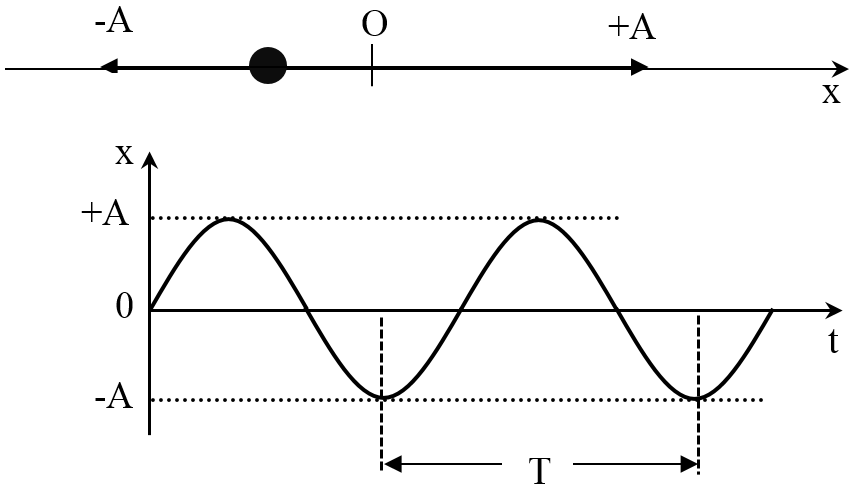
Phương trình được biểu diễn bởi đồ thị li độ theo thời gian là một đường hình sin và gọi là dao động hình sin.
Trục tung biểu diễn li độ của dao động biến thiên trong khoảng từ −A đến A, trục hoành là trục thời gian, với T là chu kỳ của dao động.
- Đồ thị biểu diễn sự phụ thuộc của x và v
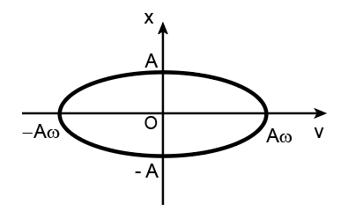
- Đồ thị biểu diễn sự phụ thuộc của v và a
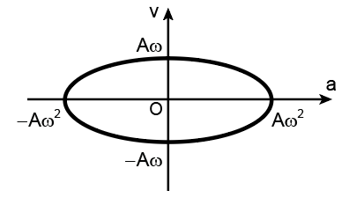
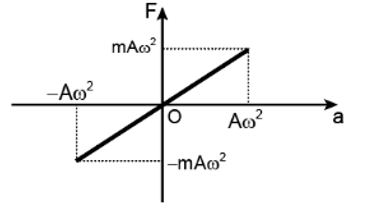
- Đồ thị biểu diễn sự phụ thuộc của a và x
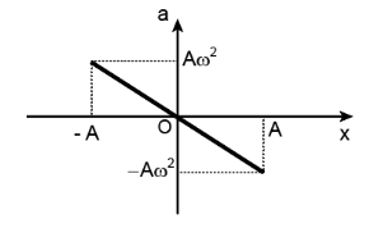
- Đồ thị biểu diễn sự phụ thuộc của F và a