Chọn đáp án đúng:
Rút gọn biểu thức
A.
B. 29
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
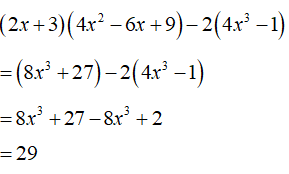
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Chọn đáp án đúng
Biểu thức viết dưới dạng bình phương của một hiệu là:
Chọn đáp án đúng:
Biết a+b=-5 và ab=6. Giá trị của biểu thức là:
Chọn đáp án đúng
Kết quả của phép phân tích đa thức thành nhân tử:
1. Nhân đơn thức với đa thức
Quy tắc: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
Tổng quát: Với A, B, C là các đơn thức, ta có: A.(B + C) = A.B + A.C.
Ví dụ:
.
Chú ý: Ta thường sử dụng các phép toán liên quan đến lũy thừa sau khi thực hiện phép nhân:
Với m, n là các số tự nhiên, a ≠ 0, ta có:
(với m ≥ n)
2. Nhân đa thức với đa thức
Quy tắc: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Tổng quát: Với A, B, C, D là các đơn thức, ta có:
(A + B)(C + D) = AC + AD + BC + BD.
Nhận xét: Tích của hai đa thức là một đa thức.
Ví dụ:
a)
=
=
=
=
b)
=
3. Các hằng đẳng thức đáng nhớ
3.1. Bình phương của một tổng.
Bình phương của một tổng bằng bình phương số thứ nhất cộng hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.
Với A, B là các biểu thức tùy ý, ta có:
Ví dụ:
3.2. Bình phương của một hiệu.
Bình phương của một hiệu bằng bình phương số thứ nhất trừ hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.
Với A, B là các biểu thức tùy ý, ta có:
Ví dụ:.
3.3. Hiệu hai bình phương.
Hiệu hai bình phương bằng tích của hiệu với tổng của chúng.
Với A, B là các biểu thức tùy ý, ta có:
Ví dụ:
3.4. Lập phương của một tổng.
Lập phương của một tổng bằng lập phương số thứ nhất cộng ba lần tích của bình phương số thứ nhất nhân số thứ hai cộng ba lần tích của số thứ nhất nhân bình phương số thứ hai cộng lập phương số thứ hai.
Với A, B là các biểu thức tùy ý, ta có:
Ví dụ:
3.5. Lập phương của một hiệu.
Lập phương của một hiệu bằng lập phương số thứ nhất trừ ba lần tích của bình phương số thứ nhất nhân số thứ hai cộng ba lần tích của số thứ nhất nhân bình phương số thứ hai trừ lập phương số thứ hai.
Với A, B là các biểu thức tùy ý, ta có:
Ví dụ:
.
3.6. Tổng hai lập phương.
Tổng của lập phương hai biểu thức bằng tích của tổng hai biểu thức và bình phương thiếu của hiệu hai biểu thức đó.
Với A, B là các biểu thức tùy ý, ta có:
Chú ý: được gọi là bình phương thiếu của một hiệu.
Ví dụ:
3.7. Hiệu hai lập phương.
Hiệu của lập phương hai biểu thức bằng tích của hiệu hai biểu thức và bình phương thiếu của tổng hai biểu thức đó.
Với A, B là các biểu thức tùy ý, ta có:
Chú ý: được gọi là bình phương thiếu của một tổng.
Ví dụ:
4. Phân tích đa thức thành nhân tử
Khái niệm: Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.
4.1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
Phương pháp: Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.
- Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.
Ví dụ:
a)
b)
Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử (lưu ý tới tính chất A = – (– A)).
Ví dụ:
4.2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
Khi áp dụng phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử, ta cần lưu ý:
- Trước tiên nhận xét xem các hạng tử của đa thức có chứa nhân tử chung không, nếu có thì áp dụng phương pháp đặt thành nhân tử chung.
- Nếu không thì ta có thể sử dụng các hằng đẳng thức sau đây để phân tích đa thức thành nhân tử:
1)
2)
3)
4)
5)
6)
7)
Ví dụ: Phân tích đa thức thành nhân tử.
Lời giải:
=
=
=
=
=
4.3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử là cách nhóm các hạng tử phù hợp nhằm xuất hiện nhân tử chung hoặc sẻ dụng các hằng đẳng thức.
- Ta vận dụng phương pháp nhóm hạng tử khi không thể phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung hay bằng phương pháp dùng hằng đẳng thức.
Ví dụ: Phân tích đa thức thành nhân tử.
Lời giải:
=
= x(x – 4) + y(x – 4)
= (x – 4)(x + y)
4.4. Phân tích đa thức thành nhân tử bằng các phối hợp nhiều phương pháp
Khi thực hiện phân tích đa thức thành nhân tử các biểu thức phức tạp ta thường sử dụng phối hợp cả ba phương pháp phân tích đa thức thành nhân tử cơ bản: phương pháp nhân tử chung, phương pháp hằng đẳng thức, phương pháp nhóm hạng tử.
Chú ý: Nếu các hạng tử của đa thức có nhân tử chung thì ta nên sử dụng phương pháp đặt nhân tử chung trước để đa thức trở lên đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.
Ví dụ: Phân tích đa thức thành nhân tử.
Lời giải:
=
=
=
5. Chia đơn thức cho đơn thức
Khái niệm: Cho A và B là hai đơn thức, B ≠ 0.
Ta nói đơn thức A chia hết cho đơn thức B nếu tìm được một đơn thức Q sao cho
A = B.Q
A được gọi là đơn thức bị chia, B được gọi là đơn thức chia, Q được gọi là đơn thức thương.
Kí hiệu: Q = A : B hoặc .
Nhận xét: Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
Quy tắc: Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:
- Chia hệ số của đơn thức A cho hệ số của đơn thức B.
- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
- Nhân các kết quả vừa tìm được với nhau.
Chú ý: Với mọi x ≠ 0, m, n ∈ ℕ, m ≥ n thì
nếu m > n
nếu m = n.
Ví dụ:
a)
b)
6. Chia đa thức cho đơn thức
Quy tắc: Muốn chia đa thức A cho đơn thức B (trường hợp các hạng tử của đa thức A đều chia hết cho B) ta làm như sau:
- Chia lần lượt từng hạng tử của đa thức A cho đơn thức B;
- Cộng các kết quả tìm được lại với nhau.
Chú ý: Trong thực hành ta có thể nhẩm và bỏ bớt một số phép tính trung gian.
Ví dụ:
=
.
Chú ý: Trường hợp đa thức A có thể phân tích thành nhân tử, ta thường phân tích A trước để rút gọn cho nhanh.
Ví dụ:
=
=
7. Chia đa thức một biến đã sắp xếp
7.1. Phép chia hết:
- Phép chia hết là phép chia có đa thức dư bằng 0.
Quy tắc chia:
+ Sắp xếp các đa thức theo thứ tự giảm dần của biến.
+ Lấy hạng tử cao nhất của đa thức bị chia chia cho hạng tử cao nhất của đa thức chia ta được thương 1.
+ Nhân thương 1 với đa thức chia và lấy đa thức bị chia trừ đi tích đó.
+ Lấy hạng tử cao nhất của đa thức vừa tìm được chia cho hạng tử cao nhất đa thức chia ta được thương 2.
+ Tiếp tục lặp lại các bước trên đến khi nhận được hiệu bằng 0.
Ví dụ: Làm tính chia: .
Lời giải:
Ta có:
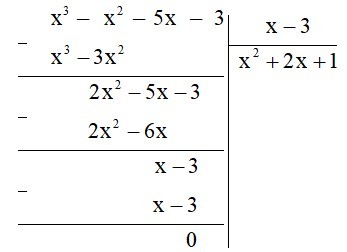
Vậy
7.2. Phép chia có dư:
- Phép chia có dư là phép chia có đa thức dư khác 0.
Quy tắc chia: Làm tương tự phép chia hết đến khi thu được đa thức dư có bậc nhỏ hơn bậc của đa thức chia.
Chú ý: Với hai đa thức tùy ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q + R, trong đó R = 0 hoặc bậc của R nhỏ hơn bậc của B (R được gọi là dư trong phép chia A cho B).
Khi R = 0 phép chia A cho B là phép chia hết.
Ví dụ: Làm tính chia:
Lời giải:
Ta có:
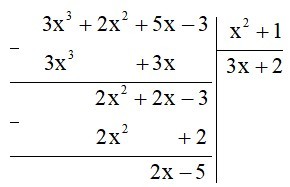
Vậy (dư 2x – 5)
Hay