Cho M (0; 2), N (1; 0), P (−1; −1) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC. Phương trình đường thẳng AB của tam giác ABC là:
A. y = −2x + 3
B. y = 2x + 3
C. y = −2x – 3
D. y = 2x – 1
 Giải bởi Vietjack
Giải bởi Vietjack

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm m để 2 đường thẳng d: y = 2x + m + 3; d’: y = −4x – m – 2 cắt nhau tại 1 điểm thuộc trục hoành.
Tìm m để giao điểm của d: y = 12x + 5 – m; d’: y = 3x + m + 3 nằm bên trái trục tung.
Tìm m để giao điểm của d: mx + 2y = 5; d’: y = −2x + 1 nằm ở góc phần tư thứ nhất.
Cho đường thẳng d1: y = 2x + 6 cắt Ox; Oy theo thứ tự A và B. Diện tích tam giác OAB là
Cho đường thẳng d: y = x + 2; d’: y = −2x + 5. Gọi M là giao điểm của d và d’. A và B lần lượt là giao điểm của d và d’ với trục hoành. Khi đó, diện tích tam giác AMB là:
Cho đường thẳng d’: y = −2x + 6. Gọi M, N lần lượt là giao điểm của d’ với Ox và Oy. Khi đó, chu vi tam giác OMN là:
Giá trị của m để đường thẳng y = (m – 1)x – m cắt trục tung tại điểm có tung độ là 1 +
Đường thẳng d: y = ax + b đi qua điểm A (2; −1) và M. Biết M thuộc đường thẳng d’: 2x + y = 3 và điểm M có hoành độ bằng 0,5. Khi đó a nhận giá trị là:
Cho đường thẳng d: y = x – 1. Khi đó khoảng cách từ gốc tọa độ đến đường thẳng đã cho là:
Tìm m để đường thẳng (d): 2y + x – 7 = 0; (d’): y = 3; (d’’): y = mx – 1 đồng quy.
Cho M (0; 2), N (1; 0), P (−1; −1) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC. Viết phương trình đường trung trực của đoạn thẳng AB.
1. Khái niệm hàm số
• Nếu đại lượng y phụ thuộc vào một đại lượng x thay đổi sao cho mỗi giá trị của x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số
• Hàm số có thể được cho bằng bảng hoặc bằng công thức, ...
• Hàm số thường được ký hiệu bởi những chữ f, g, h, ... chẳng hạn khi y là hàm số của biến số x, ta viết y = f(x) hoặc y = g(x), ….
• f(a) là giá trị của hàm số y = f(x) tại x = a. Khi hàm số y được cho bởi công thức y = f(x), muốn tính giá trị f(a) của hàm số tại x = a, ta thay x = a vào biểu thức f(x) rồi thực hiện các phép tính trong biểu thức.
• Khi x thay đổi mà y luôn nhận một giá trị không đổi thì y được gọi là một hàm hằng.
2. Đồ thị của hàm số
Tập hợp các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ được gọi là đồ thị của hàm số y = f(x).
3. Hàm số đồng biến, nghịch biến
Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc R.
• Nếu giá trị của biến x tăng lên mà giá trị của f(x) tương ứng cũng tăng lên thì hàm số y = f(x) được gọi là hàm số đồng biến trên R (gọi tắt là hàm số đồng biến).
• Nếu giá trị của biến x tăng lên mà giá trị của f(x) tương ứng giảm đi thì hàm số y = f(x) được gọi là hàm số nghịch biến trên R (gọi tắt là hàm số nghịch biến).
Nói cách khác, cho hàm số y = f(x) xác định trên tập số thực R. Với ta có:
+ Nếu x1 < x2 mà f(x1) < f(x2) thì hàm số đồng biến.
+ Nếu x1 < x2 mà f(x1) > f(x2) thì hàm số nghịch biến.
4. Định nghĩa hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số cho trước và a ≠ 0.
Chú ý: Khi b = 0 ta có hàm số y = ax (đã học ở lớp 7).
5. Tính chất hàm số bậc nhất
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có các tính chất như sau:
• Đồng biến trên R khi a > 0.
• Nghịch biến trên R khi a < 0.
6. Đồ thị hàm số y = ax + b (a ≠ 0)
Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:
- Cắt trục tung tại điểm có tung độ bằng b.
- Song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0
Chú ý. Đồ thị hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.
7. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)
• Khi b = 0 thì y = ax. Đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).
• Xét trường hợp y = ax + b với a ≠ 0 và b ≠ 0.
Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.
Cho y = 0 thì , ta được điểm thuộc trục hoành Ox.
Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0).
Chú ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.
8. Đường thẳng song song
Hai đường thẳng y = ax + b (a ≠ 0) và y = a'x + b' (a' ≠ 0) song song với nhau khi và chỉ khi a = a', b ≠ b' và trùng nhau khi và chỉ khi a = a', b = b'.
9. Đường thẳng cắt nhau
Hai đường thẳng y = ax + b (a ≠ 0) và y = a'x + b' (a' ≠ 0) cắt nhau khi và chỉ khi a ≠ a'.
Chú ý. Khi a ≠ a' và b = b' thì hai đường thẳng có cùng tung độ gốc, do đó chúng cắt nhau tại một điểm trên trục tung có tung độ là b.
10. Khái niệm hệ số góc của đường thẳng y = ax + b (a ≠ 0)
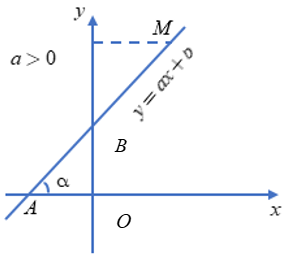
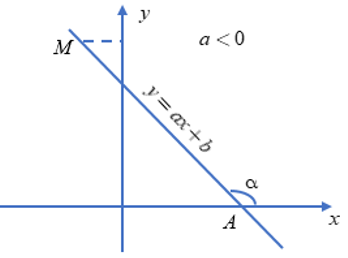
a. Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) với trục Ox
Gọi A là giao điểm của đường thẳng y = ax + b với trục Ox và M là một điểm thuộc đường thẳng và có tung độ dương.
Khi đó, là góc tạo bởi đường thẳng y = ax + b với trục Ox.
11. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)
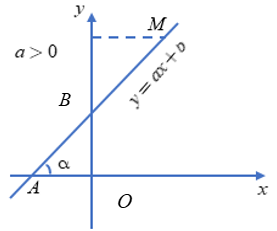
− Các đường thẳng có cùng hệ số a (a là hệ số của x) thì tạo với trục Ox các góc bằng nhau.
Khi a > 0, góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn và nếu a càng lớn thì góc đó càng lớn nhưng vẫn nhỏ hơn 90°.
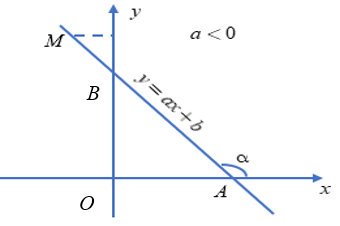
Khi a < 0 góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù và nếu a càng lớn thì góc đó càng lớn nhưng vẫn nhỏ hơn 180°.
Như vậy, góc tạo bởi đường thẳng y = ax + b và trục Ox phụ thuộc vào a.
Người ta gọi a là hệ số góc của đường thẳng y = ax + b.
Chú ý. Khi b = 0, ta có hàm số y = ax. Trong trường hợp này, ta có thể nói a là hệ số góc của đường thẳng y = ax.