Điền vào chỗ chấm để được khai triển đúng:
 Giải bởi Vietjack
Giải bởi Vietjack
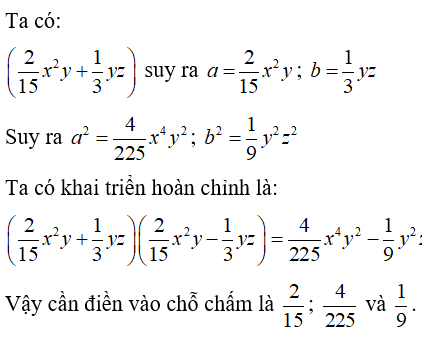
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Lựa chọn đáp án đúng nhất:
Biểu thức luôn chia hết cho 9 với mọi , đúng hay sai?
1. Bình phương của một tổng.
Bình phương của một tổng bằng bình phương số thứ nhất cộng hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.
Với A, B là các biểu thức tùy ý, ta có: .
2. Bình phương của một hiệu.
Bình phương của một hiệu bằng bình phương số thứ nhất trừ hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.
Với A, B là các biểu thức tùy ý, ta có: .
3. Hiệu hai bình phương.
Hiệu hai bình phương bằng tích của hiệu với tổng của chúng.
Với A, B là các biểu thức tùy ý, ta có: .