Tìm tham số m để đường thẳng d: y = mx + 2 cắt parabol (P): tại hai điểm phân biệt
A. m = 2
B. m = −2
C. m = 4
D. m
 Giải bởi Vietjack
Giải bởi Vietjack

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm tham số m để đường thẳng d: y = 2x – 3m – 1 tiếp xúc với parabol (P): y = −x2
Giả sử x1; x2 là hai nghiệm của phương trình x2 – 4x – 9 = 0. Khi đó x12 + x22 bằng:
Cho phương trình bậc hai: x2 – qx + 50 = 0. Tìm q > 0 và 2 nghiệm x1; x2 của phương trình biết rằng x1 = 2x2
Tìm tham số m để đường thẳng d: y = −2 (m + 1)x m2 cắt parabol (P): y = −2x2 tại hai điểm phân biệt
Cho phương trình bậc hai: x2 – 2px + 5 = 0 có 1 nghiệm x1 = 2. Tìm giá trị của p và nghiệm x2 còn lại.
1. Hàm số y = ax2
a) Tập xác định
Cho hàm số
Tập xác định của hàm số là R.
b) Tính chất
+ Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
+ Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Đồ thị của hàm số là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol đỉnh O (với O là gốc tọa độ).
Tính chất của đồ thị:
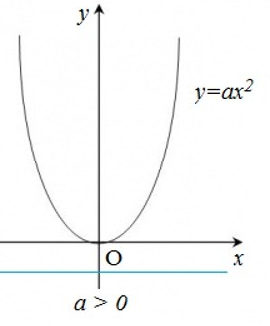
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
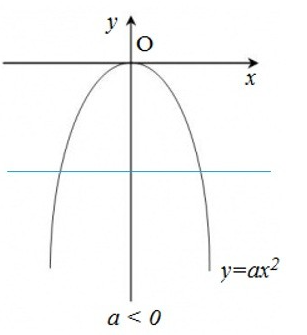
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
2. Phương trình bậc hai một ẩn
a) Định nghĩa: Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng
![]()
trong đó x là ẩn, a, b, c là những số cho trước gọi là các hệ số và .
b) Biệt thức
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) ta có biệt thức Δ như sau:
Δ = b2 - 4ac
Ta sửa dụng biết thức Δ để giải phương trình bậc hai.
c) Công thức nghiệm của phương trình bậc hai
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và biệt thức Δ = b2 - 4ac
+ Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt là
+ Nếu Δ = 0 thì phương trình có nghiệm kép là
+ Nếu Δ < 0 thì phương trình vô nghiệm.
d) Biệt thức
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và b = 2b’ ta có biệt thức như sau:
= b’2 - ac
Ta sửa dụng biết thức để giải phương trình bậc hai.
e) Công thức nghiệm thu gọn của phương trình bậc hai
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) có b = 2b’ và biệt thức = b’2 - ac
+ Nếu > 0 thì phương trình có hai nghiệm phân biệt là
+ Nếu = 0 thì phương trình có nghiệm kép là
+ Nếu < 0 thì phương trình vô nghiệm.
3. Hệ thức Vi – ét
a) Hệ thức Vi – ét
Nếu x1, x2 là hai nghiệm của phương trình ax2 + bx + c = 0 (a ≠ 0) thì ta có:
b) Ứng dụng của hệ thức Vi - ét
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x1 = 1 và nghiệm còn lại là
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a - b + c = 0 thì phương trình có một nghiệm là x1 = -1 và nghiệm còn lại là
+ Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình bậc hai x2 - Sx + P = 0
+ Điều kiện để có hai số đó là S2 - 4P ≥ 0