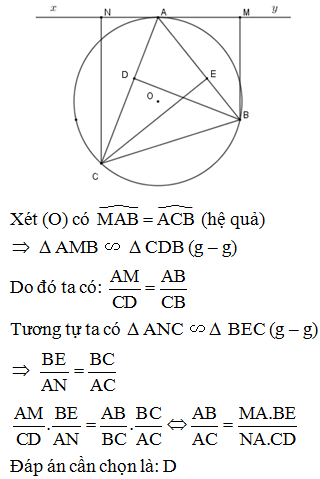
Cho tam giác nhọn ABC (AB < AC) nội tiếp (O; R). Gọi BD, CE là hai đường cao của tam giác. Gọi d là tiếp tuyến tại A của (O; R) và M, N lần lượt là hình chiếu của B, C trên d. Hệ thức nào dưới đây đúng?

Từ điểm M nằm ngoài (O) kẻ các tiếp tuyến MD; MB và cát tuyến MAC với đường tròn (A nằm giữa M và C). Hệ thức nào dưới đây là đúng?

Cho tam giác ABC nội tiếp đường tròn (O), tiếp tuyến tại A của (O) cắt BC tại P. Tia phân giác trong góc A cắt BC và (O) lần lượt tại D và M. Khi đó MA. MD bằng:

Cho nửa đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy một điểm M. Vẽ tiếp tuyến MC với nửa đường tròn. Gọi H là hình chiếu của C lên AB. Biết MC = a, MB = 3a. Độ dài đường kính AB là?

Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc. Gọi I là điểm trên cung AC sao cho khi vẽ tiếp tuyến qua I và cắt DC kéo dài tại M thì  $\widehat{CIM}$= 30^o. Số đo góc AOI là:

Cho nửa đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn. Gọi H là hình chiếu của C trên AB. Giả sử OA = 3cm; MC = 6cm. Độ dài CH là:

Cho tam giác MNP nội tiếp đường tròn (O), tiếp tuyến tại M của (O) cắt NP tại E. EM = 4cm. Tia phân giác trong góc M cắt NP và (O) lần lượt tại I và D. Chọn câu đúng?

Cho nửa đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn. Gọi H là hình chiếu của C trên AB. Giả sử $\widehat{CBA}$ = 30^o. Chọn câu sai:

Cho tam giác MNP nội tiếp đường tròn (O), tiếp tuyến tại M của (O) cắt NP tại E. EM = 4cm. Tích EP. EN bằng:

Cho tam giác giác nhọn ABC (AB < AC) nội tiếp (O; R). Gọi BD, CE là hai đường cao của tam giác. Gọi xy là tiếp tuyến tại A của (O; R) và I, K lần lượt là hình chiếu của B, C trên xy. Tam giác IAC đồng dạng với tam giác?