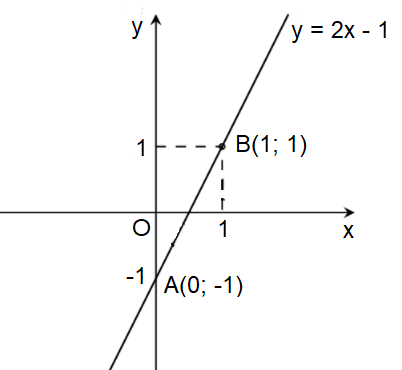Đồ thị hàm số y = b là

1. Đồ thị hàm số y = ax + b (a ≠ 0)

Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:

- Cắt trục tung tại điểm có tung độ bằng b.

- Song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0

Chú ý. Đồ thị hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.

Ví dụ 1. Gọi A là giao điểm của hai đường thẳng y = x − 1 và y = 3x + 1, tìm tọa độ của điểm A?

Lời giải:

Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:

x − 1 = 3x + 1

$\iff$3x − x = − 1 − 1

$\iff$ 2x = − 2

$\iff$ x = − 1.

Với x = − 1 thì y = − 1 − 1 = − 2. Khi đó, A(− 1; − 2).

Vậy tọa độ giao điểm A(− 1; − 2).

2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)

• Khi b = 0 thì y = ax. Đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).

• Xét trường hợp y = ax + b với a ≠ 0 và b ≠ 0.

Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.

Cho y = 0 thì $x=\frac{-b}{a}$, ta được điểm $Q(-\frac{b}{a};0)$ thuộc trục hoành Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0).

 Chú ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.

Ví dụ 2. Vẽ đồ thị hàm số y = 2x – 1.

Bước 1: Cho x = 0 thì y = −1, ta được điểm A(0; −1) ∈ Oy.

Cho y = 1 thì 2x – 1 = 1 $\iff$ x = 1, ta được điểm B(1; 1)

Bước 2: Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = 2x – 1.

Ta có đồ thị hàm số: