Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng nhất.
A. OA + OB + OC + ODAB + BC + CD + DA.
B. .
C. Cả A và B đều đúng.
D. Cả A và B đều sai.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án cần chọn là:C
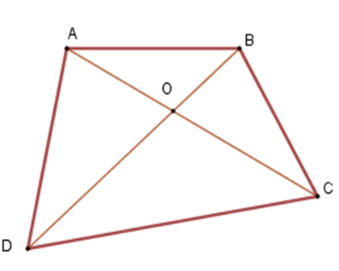
+ Xét tam giác OAB ta có OA + OB AB (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).
Tương tự ta có OC + OD CD; OB + OC BC; OA + OD AD
Cộng vế với vế ta được
OA + OB + OC + OD + OB + OC + OA + OD AB + BC + CD + AD
2(OA + OB + OC + OD) AB + BC + CD + DA
OA + OB + OC + OD nên B đúng
+ Xét tam giác ABC có AB + BC AC (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).
Tương tự ta có BC + CD BD; CD + DA AC; AD + DB BD
Cộng vế với vế ta được
AB + BC + BC + CD + CD + DA + DA + AB AC + BD + AC + BD
2(AB + BC + CD + DA) 2(AC + BD)
AB + BC + CD + DA AC + BD mà AC + BD = OA + OC + OB + OD nên
OA + OB + OC + OD AB + BC + CD + DA nên A đúng
Vậy cả A, B đều đúng.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tứ giác ABCD biết số đo của các góc tỉ lệ thuận với 4; 3; 5; 6. Khi đó số đo các góc lần lượt là:
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D = 4:3:2:1. Số đo các góc theo thứ tự đó là ?
Cho tứ giác ABCD biết số đo của các góc tỉ lệ thuận với 4; 9; 7; 6. Khi đó số đo các góc lần lượt là :
Tứ giác ABCD có . Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đô góc BID.
Tam giác ABC có các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc .
1. Định nghĩa tứ giác
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
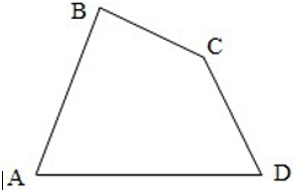
- Tứ giác ABCD còn được gọi tên là tứ giác BCDA, ADCB, ....
- Các điểm A, B, C, D được gọi là các đỉnh.
- Các đoạn thẳng AB, BC, CD, DA được gọi là các cạnh.
- Tứ giác ABCD trên hình gọi là tứ giác lồi.
• Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.
Chú ý. Khi nói đến tứ giác, ta hiểu đó là tứ giác lồi.
Ví dụ: Cho ABCD là tứ giác lồi.
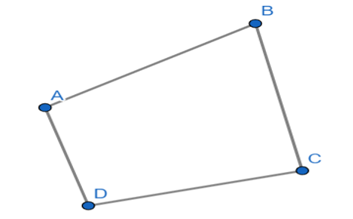
Khi đó, tứ giác nằm trong nửa mặt phẳng có bờ là đường thẳng chứa AB, BC, CD hoặc DA của tứ giác ABCD.
2. Tổng các góc của một tứ giác
Định lí. Tổng các góc của một tứ giác bằng .
Ví dụ: Cho tứ giác ABCD trong đó có = 50o, = 140o, = 75o. Tính số đo của góc ?
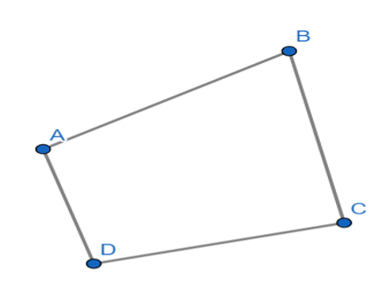
Hướng dẫn giải
Tứ giác ABCD ta có:
Vậy = .