Cho hình thang cân ABCD (AB//CD), gọi E là giao điểm của AC và BD. Tìm mệnh đề sai ?
A.
B.
C. tam giác ABE cân
D. tam giác AED cân
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình thang cân ABCD có AB// CD và AB = BC. Tìm khẳng định sai.
Cho hình thang ABCD có AB // CD , hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD . Tìm khẳng định sai trong các khẳng định sau?
Điền chữ “Đ” hoặc “S” vào mỗi câu khẳng định sau:
A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
B. Hình thang cân có hai cạnh bên bằng nhau.
C. Hình thang cân có hai góc kề một cạnh đáy bù nhau.
D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
Điền cụm từ thích hợp vào chỗ trống
A. Hình thang cân là…………………………………..
B. Hình thang có………………. là hình thang cân .
C. Hai cạnh bên của hình thang cân…………………..
D. Hình thang cân có hai góc kề một đáy…………….
Cho hình thang cân ABCD có AB // CD. Gọi giao điểm của AD và BC là M . Tam giác MCD là tam giác gì ?
1. Định nghĩa
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Ví dụ 1. Tứ giác ABCD là hình thang cân (đáy AB, CD) thì:
+ AB // CD
+ (hoặc ).
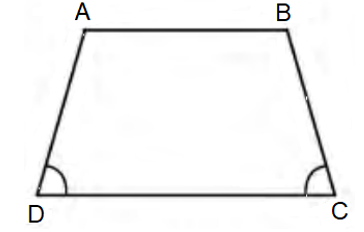
Chú ý. Nếu ABCD là hình thang cân (đáy AB, CD) thì và .
2. Tính chất
Định lí 1. Trong một hình thang cân, hai cạnh bên bằng nhau.
Ví dụ 2: ABCD là hình thang cân có đáy AB và CD.
Khi đó, AD và BC là hai cạnh bên.
Do đó, AD = BC.
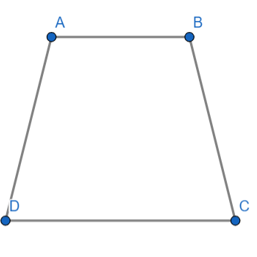
Định lí 2. Trong một hình thang cân, hai đường chéo bằng nhau.
Ví dụ 3: ABCD là hình thang cân (đáy AB, CD) có AC và BD là hai đường chéo.
Khi đó, AC = BD.
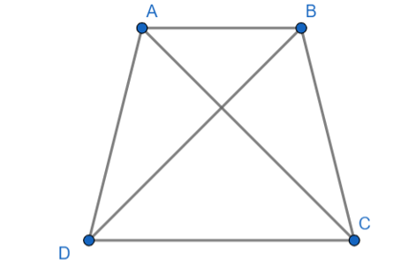
3. Dấu hiệu nhận biết
Định lí 3. Hình thang có hai đường chéo bằng nhau là hình thang cân.
Ví dụ 4: Hình thang ABCD (đáy AB, CD) có AC, BD là hai đường chéo và AC = BD.
Khi đó, ABCD là hình thang cân.

Dấu hiệu nhận biết hình thang cân:
- Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
Ví dụ 6: Hình thang cân ABCD có AB // CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh rằng: DH = CK.
Hướng dẫn giải
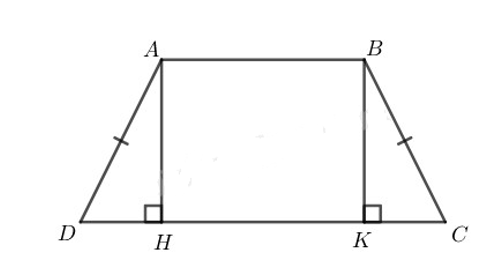
Xét ∆AHD và ∆BKC có:
AD = BC (tính chất hình thang cân)
(tính chất hình thang cân)
Do đó, ΔAHD = ΔBKC (cạnh huyền - góc nhọn).
Suy ra HD = KC (hai góc tương ứng).
Từ đó ta có điều phải chứng minh.