Cho tam giác ABC, điểm H di chuyển trên cạnh BC. Gọi O là trung điểm của AH. Mệnh đề nào sau đây là đúng?
A. Điểm O di chuyển trên đường trung trực của BC
B. Điểm O di chuyển trên đường trung tuyến ứng với cạnh đáy AB
C. Điểm O di chuyển trên đường trung bình của tam giác ABC
D. Điểm O di chuyển một đường thẳng bất kỳ không xác định
 Giải bởi Vietjack
Giải bởi Vietjack
Qua O kẻ đường thẳng song song với BC, cắt AB và AC theo thứ tự ở M và N.
Tam giác ABH có nên M là trung điểm của AB.
Tam giác ACH có nên N là trung điểm của AC.
Suy ra MN là đường trung bình của tam giác ABC.
Các điểm M, N cố định. Vậy điểm O di chuyển trên đoạn thẳng MN hay điểm O di chuyển trên đường trung bình của tam giác ABC.
Chọn C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường thẳng xy. Một điểm M cố định nằm ngoài xy và một điểm N di động trên xy. Kẻ , gọi I là trung điểm của MN. Khẳng định nào sau đây là đúng?
Cho điểm P nằm ngoài đường thẳng d và khoảng cách đến d bằng 3cm. Trên d lấy một điểm N bất kỳ. Gọi M là điểm đối xứng với điểm P qua điểm N. Khi đó, độ dài của ME là
1. Khoảng cách giữa hai đường thẳng song song
Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia.
Ví dụ: Cho hai đường thẳng song song a và b. Gọi A và B là hai điểm bất kỳ thuộc đường thẳng a, AH và BK là các đường vuông góc kẻ từ A và b đến đường thẳng b.
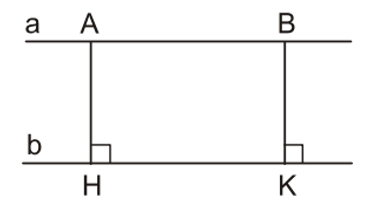
Khi đó, AH và BK lần lượt là khoảng cách từ điểm A và B đến đường thẳng b.
2. Tính chất của các điểm cách đều một đoạn thẳng cho trước
Tính chất. Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h.
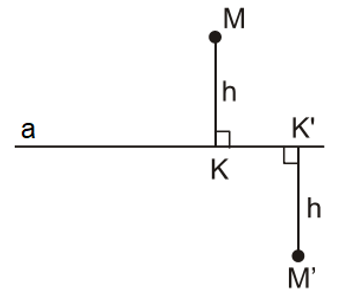
Ví dụ: Cho hai điểm M và M’ đều cách b một khoảng bằng h. Gọi MK và M’K’ lần lượt là khoảng cách từ hai điểm M và M’ đến đường thẳng a.
Khi đó, MK // M’K’.
Nhận xét: Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.
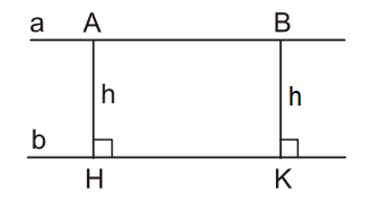
Ví dụ: Các điểm cách đường thẳng cố định b một khoảng bằng h không đổi. Khi đó, các điểm này nằm trên đường thẳng a // b và cách đường thẳng b một khoảng bằng h
3. Đường thẳng song song cách đều
Định lí:
• Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
• Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
Ví dụ: Các đường thẳng a, b, c, d song song cách đều và cắt đường thẳng AD lần lượt tại các điểm A, B, C, D.
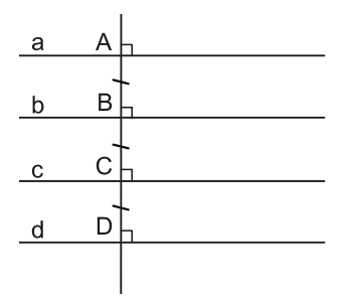
Khi đó, AB = BC = CD.