Cho góc vuông $\widehat{xOy}$. Trên Ox lấy điểm B sao cho OB = 5cm. Điểm D di động trên Oy. Vẽ tam giác BCD vuông cân tại B sao cho điểm C nằm trong góc vuông $\widehat{xOy}$. 

Khẳng định nào sau đây là đúng?

1. Khoảng cách giữa hai đường thẳng song song

Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia.

Ví dụ: Cho hai đường thẳng song song a và b. Gọi A và B là hai điểm bất kỳ thuộc đường thẳng a, AH và BK là các đường vuông góc kẻ từ A và b đến đường thẳng b.

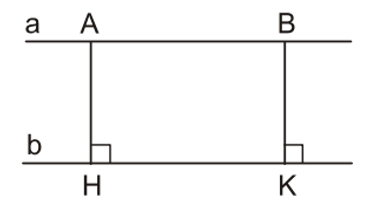
Khi đó, AH và BK lần lượt là khoảng cách từ điểm A và B đến đường thẳng b.

2. Tính chất của các điểm cách đều một đoạn thẳng cho trước

Tính chất. Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h.

Ví dụ: Cho hai điểm M và M’ đều cách b một khoảng bằng h. Gọi MK và M’K’ lần lượt là khoảng cách từ hai điểm M và M’ đến đường thẳng a.

Khi đó, MK // M’K’.

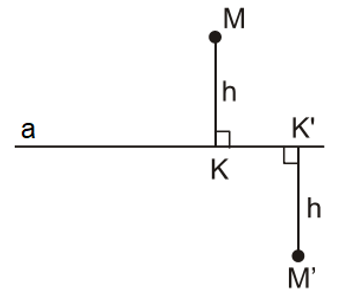
Nhận xét: Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.

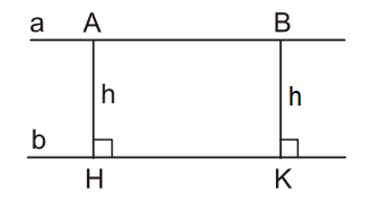
Ví dụ: Các điểm cách đường thẳng cố định b một khoảng bằng h không đổi. Khi đó, các điểm này nằm trên đường thẳng a // b và cách đường thẳng b một khoảng bằng h

3. Đường thẳng song song cách đều

Định lí:

• Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.

• Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.

Ví dụ: Các đường thẳng a, b, c, d song song cách đều và cắt đường thẳng AD lần lượt tại các điểm A, B, C, D.

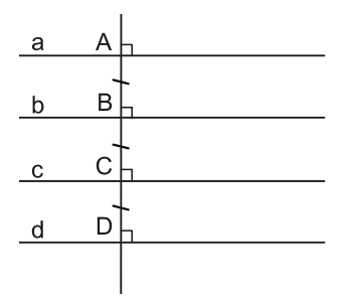
Khi đó, AB = BC = CD.