Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB, M’ là điểm đối xứng với M qua D. Tứ giác AMBM’ là hình gì?
A. Hình thoi
B. Hình chữ nhật
C. Hình bình hành
D. Hình thang
 Giải bởi Vietjack
Giải bởi Vietjack
Vì M’ đối xứng M qua D nên DM = DM’ (1)
M, D lần lượt là trung điểm của BC, AB nên MD là đường trung bình của ΔABC.
Suy ra MD // AC (2)
Mặt khác ΔABC vuông ở A nên AB ⊥ AC (2)
Từ (1) và (2) suy ra DM ⊥ AB => MM’ ⊥ AB.
Vì D là trung điểm của AB (gt) và D là trung điểm của MM’ nên tứ giác AMBM’ là hình bình hành. Mặt khác MM’ ⊥ AB nên AMBM’ là hình thoi.
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình thang ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Hình thang ABCD có thêm điều kiện gì thì MNPQ là hình thoi. Hãy chọn câu đúng.
Cho hình thoi có độ dài hai đường chéo là 12cm và 16cm. Tính độ dài cạnh hình thoi.
Cho hình bình hành ABCD. Gọi E, F là trung điểm của các cạnh AD và BC. Các đường BE, DE cắt các đường chéo AC tại P và Q. Tứ giác EPFQ là hình thoi nếu góc ACD bằng:
Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứ tự là giao điểm của AE, AF với đường chéo BD. Tứ giác AGCH là hình gì?
Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD phải có điều kiện gì thì EFGH là hình thoi?
Cho hình thoi có độ dài hai đường chéo là 24cm và 10cm. Tính độ dài cạnh hình thoi.
Cho hình thoi ABCD có góc A tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia đôi cạnh đó. Tính các góc của hình thoi.
Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứ tự là giao điểm của AE, AF với đường chéo BD. Cho OC = 4; OH = 3. Tính chu vi tứ giác AHCG.
Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB, M’ là điểm đối xứng với M qua D. Cho BC = 4cm. Tính chu vi tứ giác AMBM’.
1. Định nghĩa
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Ví dụ:
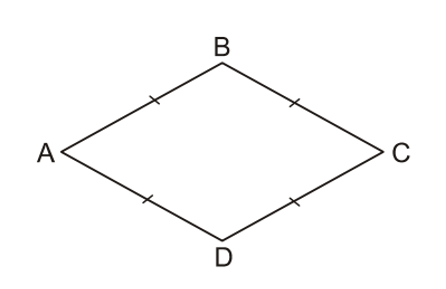
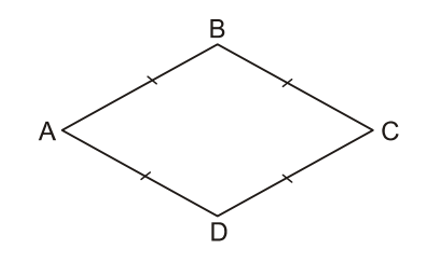
Tứ giác ABCD là hình thoi AB = BC = CD = DA.
• Hình thoi cũng là một hình bình hành.
Ví dụ:
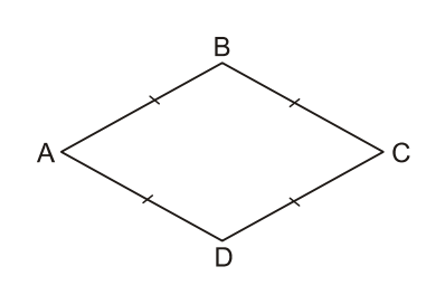
Hình thoi ABCD có AB = BC = CD = DA.
Ta thấy có hai cạnh đối nhau AB và CD; AD và BC đều bằng nhau.
Do đó ABCD là hình bình hành.
2. Tính chất
Hình thoi có tất cả các tính chất của hình bình hành.
Định lí:
Trong hình thoi:
• Hai đường chéo vuông góc với nhau.
• Hai đường chéo là các đường phân giác các góc của hình thoi.
Ví dụ:
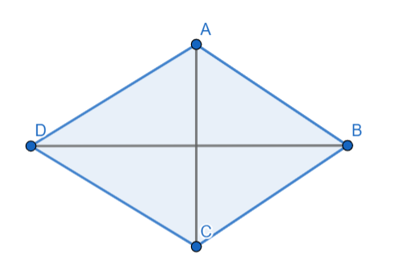
Hình thoi ABCD có AC và BD là hai đường chéo.
Khi đó, AC BD.
3. Dấu hiệu nhận biết hình thoi
• Tứ giác có bốn cạnh bằng nhau là hình thoi.
• Hình bình hành có hai cạnh kề nhau là hình thoi.
• Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
• Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Ví dụ: Cho hình bình hành ABCD có hai cạnh kề AB và BC bằng nhau. Chứng minh tứ giác ABCD là hình thoi.
Hướng dẫn giải
Tứ giác ABCD là hình bình hành nên:
AB = CD; BC = DA.
Mặt khác, AB = BC.
Do đó AB = BC = CD = DA.
Khi đó tứ giác ABCD có AB = BC = CD = DA.
Vậy tứ giác ABCD là hình thoi.