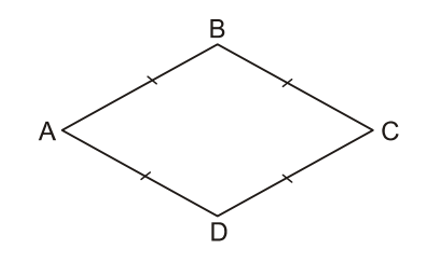
Cho tứ giác ABCD có = 500, = 800, AD = BC. Gọi E, F lần lượt là trung điểm của các cạnh AB và CD. Tính số đo góc EFC.
A. 750
B. 950
C. 1050
D. 1200
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi G, H lần lượt là trung điểm của AC, BD.
Vì E, G lần lượt là trung điểm của AB, AC nên EG là đường trung bình của tam giác ABC. Suy ra EG = BC, EG // BC.
Chứng minh tương tự ta cũng có:
GF = AD, FH = BC, HE = AD; GF // AD; FH // BC; HE // AD
Mà AD = BC (gt), nên EG = GF = FH = HE
Suy ra: tứ giác EGFH là hình thoi.
Suy ra EF là tia phân giác của góc HFG
=>
= 800 (do GF // AD);
= 500 (do FH // BC)
Do đó = 1800 – () = 500
=> = .500 = 250
Vậy = 250 + 800 = 1050
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình thoi ABCD có chu vi bằng 24 cm, đường cao AH bằng 3cm. Tính
Cho tam giác ABCD. Trên các cạnh AB và AC lần lượt lấy hai điểm D và E sao cho BD = CE. Gọi M, N, P, Q thứ tự là trung điểm của BE, CD, DE và BC. Chọn câu đúng nhất.
Cho tam giác ABC đều, H là trực tâm, đường cao AD. M là điểm bất kì trên cạnh BC. Gọi E, F lần lượt là hình chiếu của M trên AB, AC, gọi I là trung điểm của đoạn thẳng AM. ID cắt EF tại K. Chọn câu sai.
Tứ giác ABCD có AB = CD. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi I, K theo thứ tự là trung điểm của AC, BD. Chọn câu đúng nhất.
Cho hình thoi ABCD có chu vi bằng 16cm, đường cao AH bằng 2cm. Tính các góc của hình thoi. Hãy chọn câu đúng.
1. Định nghĩa
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Ví dụ:
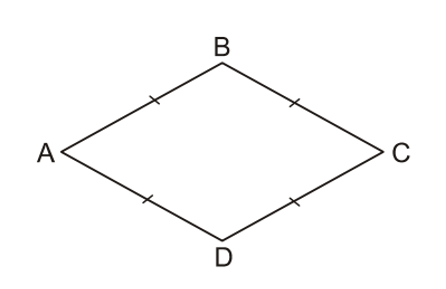
Tứ giác ABCD là hình thoi AB = BC = CD = DA.
• Hình thoi cũng là một hình bình hành.
Ví dụ:
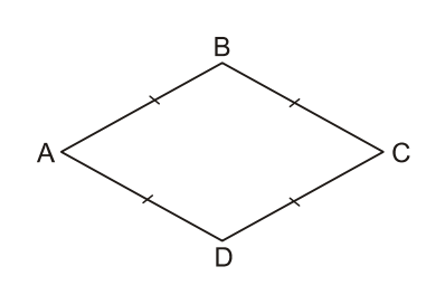
Hình thoi ABCD có AB = BC = CD = DA.
Ta thấy có hai cạnh đối nhau AB và CD; AD và BC đều bằng nhau.
Do đó ABCD là hình bình hành.
2. Tính chất
Hình thoi có tất cả các tính chất của hình bình hành.
Định lí:
Trong hình thoi:
• Hai đường chéo vuông góc với nhau.
• Hai đường chéo là các đường phân giác các góc của hình thoi.
Ví dụ:
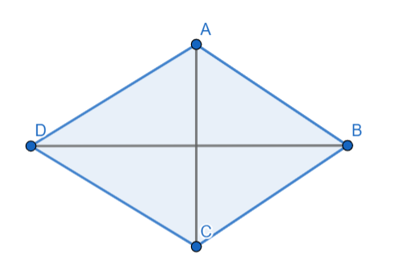
Hình thoi ABCD có AC và BD là hai đường chéo.
Khi đó, AC BD.
3. Dấu hiệu nhận biết hình thoi
• Tứ giác có bốn cạnh bằng nhau là hình thoi.
• Hình bình hành có hai cạnh kề nhau là hình thoi.
• Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
• Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Ví dụ: Cho hình bình hành ABCD có hai cạnh kề AB và BC bằng nhau. Chứng minh tứ giác ABCD là hình thoi.
Hướng dẫn giải
Tứ giác ABCD là hình bình hành nên:
AB = CD; BC = DA.
Mặt khác, AB = BC.
Do đó AB = BC = CD = DA.
Khi đó tứ giác ABCD có AB = BC = CD = DA.
Vậy tứ giác ABCD là hình thoi.