Cho tam giác ABC vuông tại A. Điểm M thuộc BC. Qua M dựng đường thẳng song song với AB cắt AC tại D. Qua M dựng đường thẳng song song với AC cắt AB tại E. Tứ giác ADME là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình vuông
Giải bởi Vietjack
Vì MD //AB; ME // AC mà AB ⊥ AC nên MD ⊥ AC; ME ⊥ AB.
Suy ra = 900 nên tứ giác DMEA là hình chữ nhật
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là các trung điểm của AB, BC, AC. Tam giác ABC cần có thêm điều kiện gì để hình chữ nhật AMNP là hình vuông?
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC. K là điểm đối xứng với M qua điểm I. Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông.
Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC. K là điểm đối xứng với M qua điểm I. Tứ giác AKMB là hình gì?
Cho hình vuông có chu vi 16 cm. Bình phương độ dài một đường chéo của hình vuông là
Cho tam giác ABC vuông tại A. Điểm M thuộc BC. Qua M dựng đường thẳng song song với AB cắt AC tại D. Qua M dựng đường thẳng song song với AC cắt AB tại E. Tìm vị trí điểm M để tứ giác ADME là hình vuông.
Cho hình vuông có chu vi 20 cm. Bình phương độ dài một đường chéo của hình vuông là:
Cho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông khi.
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC, chúng cắt AB và AC theo thứ tự tại E và F. Tứ giác EFGH là hình gì?
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC, chúng cắt AB và AC theo thứ tự tại E và F. Cho BC = 9 cm. Tính chu vi của tứ giác EFGH.
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để hình bình hành EFGH là hình vuông.
Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác 4 góc đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì?
1. Định nghĩa
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
Ví dụ:
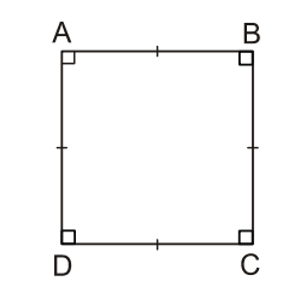
Tổng quát: ABCD là hình vuông
Nhận xét:
• Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
• Hình vuông là hình thoi có bốn góc vuông.
• Hình vuông vừa là hình chữ nhật vừa là hình thoi.
Ví dụ:
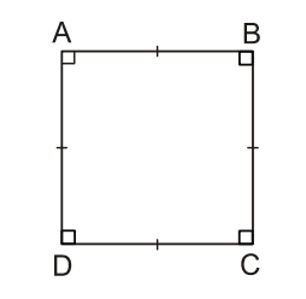
Tứ giác ABCD là hình vuông.
Khi đó, ABCD là hình chữ nhật có AB = BC = CD = DA.
2. Tính chất
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
Ví dụ:
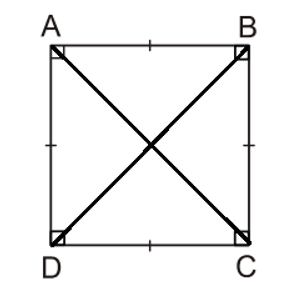
Tứ giác ABCD là hình vuông. Khi đó:
+ AB = BC = CD = DA (tính chất hình hình chữ nhật).
+ (tính chất hình hình chữ nhật).
+ Hai đường chéo AC và BD vuông góc với nhau (tính chất hình thoi).
3. Dấu hiệu nhận biết hình vuông
• Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
• Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
• Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
• Hình thoi có một góc vuông là hình vuông.
• Hình thoi có hai đường chéo bằng nhau là hình vuông.
Ví dụ: Cho tứ giác MNPQ có hai đường chéo MP và NQ cắt nhau tại O. Biết và OM = ON = OP = OQ. Chứng minh tứ giác MNPQ là hình vuông.
Hướng dẫn giải
Tứ giác MNPQ có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Nên MNPQ là hình bình hành.
Hình bình hành MNPQ có hai đường chéo bằng nhau.
Nên MNPQ là hình chữ nhật.
Hình chữ nhật MNPQ có MP ⊥ NQ tại O.
Vậy MNPQ là hình vuông.
