Cho hình bình hành ABCD có DC = 2BC. Gọi E, F là trung điểm của AB, DC. Gọi AF cắt DE tại I, BF cắt CE tại K. Chọn câu đúng nhất.
A. Tứ giác DEBF là hình bình hành.
B. Tứ giác AEFD là hình thoi
C. Tứ giác EBCF là hình vuông
D. Cả A, B đều đúng
 Giải bởi Vietjack
Giải bởi Vietjack
Xét hình bình hành ABCD có E, F lần lượt là trung điểm của AB, CD, DC = 2BC nên AE = EB = BC = CF = DF = AD; AB // CD, AD // BC
Xét tứ giác DEBF có
nên DEBF là hình bình hành
Xét tứ giác AEFD có AE = DF; AE // DF nên AEDF là hình bình hành, lại có AE = AD nên hình bình hành AEFD là hình thoi.
Tương tự ta cũng có EBCF là hình thoi. Nhận thấy chưa đủ điều kiện để EBCF là hình vuông.
Nên A, B đúng, C sai.
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hình thoi có độ dài hai đường chéo lần lượt bằng 12cm và 16cm. Độ dài cạnh hình thoi đó là:
Độ dài một cạnh hình vuông bằng 5cm. Thì độ dài đường chéo hình vuông đó sẽ là:
Một tam giác đều có độ dài cạnh bằng 14cm. Độ dài một đường trung bình của tam giác đó là:
Một hình thang cân có cạnh bên là 2,5cm; đường trung bình là 3cm. Chu vi của hình thang là:
Hình thang ABCD (AB // CD) có số đo góc D bằng 700, số đo góc A là:
Cho hình bình hành ABCD có DC = 2BC. Gọi E, F là trung điểm của AB, DC. Gọi AF cắt DE tại I, BF cắt CE tại K. Tứ giác EIFK là hình gì?
Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = 14cm. Tính độ dài MI, IK.
Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I. Tứ giác AKMB là hình gì?
Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I. Tứ giác AMCK là hình gì?
Cho hình bình hành ABCD có BC = 2AB và = 600. Gọi E, F theo thứ tự là trung điểm của BC và AD. Gọi I là điểm đối xứng với A qua B. Số đo góc AED là:
Cho hình bình hành ABCD có BC = 2AB và = 600. Gọi E, F theo thứ tự là trung điểm của BC và AD. Gọi I là điểm đối xứng với A qua B. Tứ giác BICD là hình gì?
1. Định nghĩa tứ giác
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
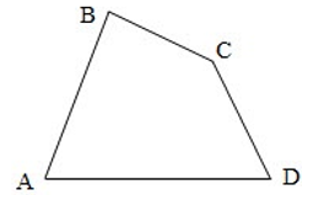
- Tứ giác ABCD còn được gọi tên là tứ giác BCDA, ADCB, ....
- Các điểm A, B, C, D được gọi là các đỉnh.
- Các đoạn thẳng AB, BC, CD, DA được gọi là các cạnh.
- Tứ giác ABCD trên hình gọi là tứ giác lồi.
• Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.
Chú ý. Khi nói đến tứ giác, ta hiểu đó là tứ giác lồi.
2. Tổng các góc của một tứ giác
Định lí. Tổng các góc của một tứ giác bằng 360.
3. Định nghĩa hình thang
Hình thang là tứ giác có hai cạnh đối song song.
Hai cạnh song song gọi là hai đáy.
Hai cạnh còn lại gọi là hai cạnh bên.
Nhận xét:
- Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
- Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
4. Hình thang vuông
Định nghĩa: Hình thang vuông là hình thang có một góc vuông.
5. Định nghĩa hình thang cân
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Chú ý. Nếu ABCD là hình thang cân (đáy AB, CD) thì
6. Tính chất hình thang cân
Định lí 1. Trong một hình thang cân, hai cạnh bên bằng nhau.
Định lí 2. Trong một hình thang cân, hai đường chéo bằng nhau.
7. Dấu hiệu nhận biết hình thang cân
Định lí 3. Hình thang có hai đường chéo bằng nhau là hình thang cân.
Dấu hiệu nhận biết hình thang cân:
- Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
8. Đường trung bình của tam giác
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Định lí 1. Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Định lí 2. Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
9. Đường trung bình của hình thang
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
Định lí 3. Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
10. Bài toán dựng hình
Ta đã biết vẽ hình bằng nhiều dụng cụ: thước, compa, êke…. Ta xét các bài toán vẽ hình mà chỉ sử dụng hai dụng cụ là thước và compa, chúng được gọi là các bài toán dựng hình.
Với thước, ta có thể:
+ Vẽ được một đường thẳng khi biết hai điểm của nó.
+ Vẽ được một đoạn thẳng khi biết hai đầu mút của nó.
+ Vẽ được một tia khi biết gốc và một điểm của tia.
Với compa, ta có thể vẽ được một đường tròn khi biết tâm và bán kính của nó.
11. Các bài toán dựng hình đã biết
Chúng ta đã biết cách giải các bài toán dựng hình sau:
+ Dựng một đoạn thẳng bằng một đoạn thẳng cho trước.
+ Dựng một góc bằng một góc cho trước.
+ Dựng đường trung trực của một đoạn thẳng cho trước, dựng trung điểm của đoạn thẳng cho trước.
+ Dựng tia phân giác của một góc cho trước.
+ Qua một điểm cho trước, dựng đường thẳng vuông góc với một đường thẳng cho trước.
+ Qua một điểm nằm ngoài một đường thẳng cho trước, dựng đường thẳng song song với một đường thẳng cho trước.
+ Các dạng dựng tam giác (biết ba cạnh, biết hai cạnh và góc xen giữa, một cạnh và hai góc kề).
12. Hai điểm đối xứng qua một đường thẳng
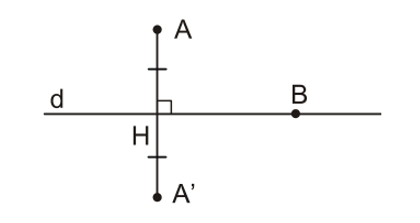
Hai điểm được gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
Quy ước: Nếu điểm B nằm trên đường thẳng d thì điểm đối xứng của B qua đường thẳng d cũng chính là điểm B.
13. Hai hình đối xứng qua đường thẳng
Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng d và ngược lại.
Đường thẳng d gọi là trục đối xứng của hai hình đó.
14. Hình có trục đối xứng
Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.
Ta nói rằng hình H có trục đối xứng.
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
15. Định nghĩa hình bình hành
Hình bình hành là tứ giác có các cạnh đối song song.
Chú ý: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song).
16. Tính chất hình bình hành
Định lí:
Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
17. Dấu hiệu nhận biết hình bình hành
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
18. Hai điểm đối xứng qua một điểm
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Quy ước: Điểm đối xứng với điểm O qua điểm O cũng là điểm O.
19. Hai hình đối xứng qua một điểm
Định nghĩa: Hai hình gọi là đối xứng với nhau qua điểm O nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm O và ngược lại.
20. Hình có tâm đối xứng
Định nghĩa: Điểm O gọi là tâm đối xứng qua hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.
Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
21. Định nghĩa hình chữ nhật
Hình chữ nhật là tứ giác có bốn góc vuông.
• Hình chữ nhật cũng là một hình bình hành và cũng là hình thang cân.
22. Tính chất hình chữ nhật
Hình chữ nhật là có tất cả các tính chất của hình bình hành và hình thang cân.
Định lí: Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
23. Dấu hiệu nhận biết hình chữ nhật
• Tứ giác có ba góc vuông là hình chữ nhật.
• Hình thang cân có một góc vuông là hình chữ nhật.
• Hình bình hành có một góc vuông là hình chữ nhật.
• Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
24. Áp dụng vào tam giác
• Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
• Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
25. Khoảng cách giữa hai đường thẳng song song
Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia.
26. Tính chất của các điểm cách đều một đoạn thẳng cho trước
Tính chất. Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h.
Nhận xét: Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.
27. Đường thẳng song song cách đều
Định lí:
• Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
• Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
28. Định nghĩa hình thoi
Hình thoi là tứ giác có bốn cạnh bằng nhau.
• Hình thoi cũng là một hình bình hành.
29. Tính chất hình thoi
Hình thoi có tất cả các tính chất của hình bình hành.
Định lí:
Trong hình thoi:
• Hai đường chéo vuông góc với nhau.
• Hai đường chéo là các đường phân giác các góc của hình thoi.
30. Dấu hiệu nhận biết hình thoi
• Tứ giác có bốn cạnh bằng nhau là hình thoi.
• Hình bình hành có hai cạnh kề nhau là hình thoi.
• Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
• Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
31. Định nghĩa hình vuông
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
Nhận xét:
• Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
• Hình vuông là hình thoi có bốn góc vuông.
• Hình vuông vừa là hình chữ nhật vừa là hình thoi.
32. Tính chất hình vuông
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
33. Dấu hiệu nhận biết hình vuông
• Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
• Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
• Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
• Hình thoi có một góc vuông là hình vuông.
• Hình thoi có hai đường chéo bằng nhau là hình vuông.