Hình tam giác vuông có 1 cạnh góc vuông giảm đi 3 lần và cạnh góc vuông còn lại tăng lên 3 lần, khi đó diện tích hình tam giác vuông mới
A. Không thay đổi
B. Tăng 3 lần
C. Giảm 6 lần
D. Giảm 3 lần
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Theo công thức tính diện tích tam giác vuông có 2 cạnh góc vuông có độ dài là a, b là S =a.b
Tam giác vuông mới có độ dài hai cạnh góc vuông a’, b’ thì theo đề bài ta có a’ =a; b’ = 3b; khi đó, diện tích S’ =a’.b’ =a.3b =ab = S
Do đó diện tích hình tam giác mới không thay đổi so với tam giác ban đầu
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hình chữ nhật có chiều dài tăng 4 lần, chiều rộng giảm 2 lần, khi đó diện tích hình chữ nhật
Hình chữ nhật có chiều dài giảm 6 lần, chiều rộng tăng 3 lần, khi đó diện tích hình chữ nhật
Hình chữ nhật có chiều dài giảm đi 5 lần, chiều rộng tăng lên 5 lần, khi đó diện tích hình chữ nhật
1. Khái niệm diện tích đa giác
• Số đo của một phần mặt phẳng giới hạn bởi một đa giác được gọi là diện tích đa giác đó.
• Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương.
Diện tích đa giác có các tính chất sau:
• Hai tam giác bằng nhau thì có diện tích bằng nhau.
• Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.
Ví dụ:
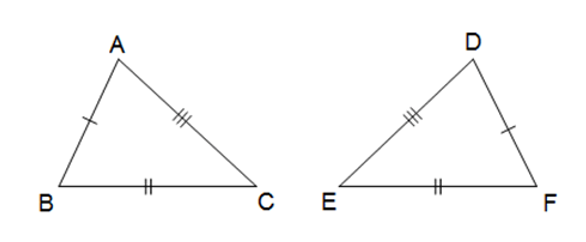
Xét ∆ABC và ∆DFE có:
AB = DF (hình vẽ)
BC = FE (hình vẽ)
AC = DE (hình vẽ)
Do đó ∆ABC = ∆DFE (c.c.c)
Suy ra SABC = SDFE.
2. Công thức diện tích hình chữ nhật
Diện tích hình chữ nhật là tích hai kích thức của nó: S = a . b
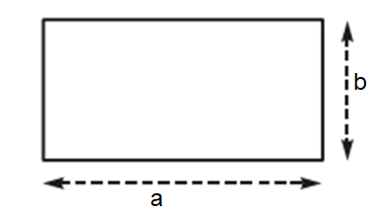
Ví dụ: Hình chữ nhật có chiều dài 16 m, chiều rộng 9 m.
Khi đó, diện tích hình chữ nhật là: 16 . 9 = 144 ().
3. Công thức diện tích hình vuông, diện tích tam giác vuông
Diện tích hình vuông bằng bình phương cạnh của nó: S = .

Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông: S = a.b.

Ví dụ: Hình vuông có độ dài một cạnh là 15.
Khi đó, diện tích hình vuông là: = 225 ().