Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Vẽ BPMN; CQMN (P, QMN). So sánh và .
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Kẻ AHBC tại H và AH cắt MN tại K.
+ Xét tam giác ABC có MN là đường trung bình nên MN // BC suy ra AHMN tại K. Xét tứ giác CBPQ có PQ // BC (do MN // BC) và PB // CQ (do cùng vuông góc với PQ) nên CBPQ là hình bình hành. Lại có = nên tứ giác CBPQ là hình chữ nhật. Suy ra = BP.BC.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình thoi MNPQ. Biết A, B, C, D lần lượt là các trung điểm của các cạnh NM, NP, PQ, QM.
Tính tỉ số diện tích của tứ giác ABCD và hình thoi MNPQ.
Cho tam giác vuông tại ABC. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Biết = 100 , tính
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Vẽ BPMN; CQMN (P, QMN). Biết , tính .QC = 75 cm2
Cho hình thoi ABCD có BD = 60 cm, AC = 80 cm. Vẽ các đường cao BE Và BF của và . Tính diện tích tứ giác BEDF.
Cho tam giác vuông tại ABC. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Chọn khẳng định đúng:
Cho hình vuông ABCD có cạnh 10m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng diện tích vuông ABCD.
Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng diện tích vuông ABCD.
1. Diện tích tứ giác có hai đường chéo vuông góc
Diện tích của một tứ giác có hai đường chéo vuông góc bằng nửa tích độ dài hai đường chéo đó.
Ví dụ: Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau.

Khi đó, diện tích tứ giác ABCD là:
SABCD = . AC . BD.
2. Công thức tính diện tích hình thoi
Diện tích hình thoi bằng nửa tích hai đường chéo.
S = d1 . d2
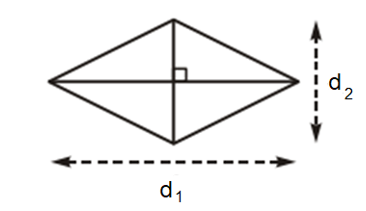
Ví dụ: Cho hình thoi có lần lượt độ dài hai đường chéo là 25 cm, 18 cm.
Khi đó, diện tích hình thoi là: S = . 25 . 18 = 225 ().