Cho tam giác ABC có diện tích là S. Trên cạnh AB, BC, CA lần lượt lấy ba điểm M, N, P sao cho AM = 2.BM, BN = 2.NC, CP = 2.PA. Tính diện tích tam giác MNP theo S.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC cân ở A, AB = AC = 5cm, BC = 6cm. Gọi O là trung điểm của đường cao AH. Các tia BO và CO cắt cạnh AC và AB lần lượt ở D và E. Tính .
Cho lục giác lồi ABCDEF có các cặp cạnh đối song song. Khẳng định nào sau đây là đúng?
Cho ABC. Lấy điểm M, N, P lần lượt thuộc cạnh AC, AB, BC sao cho Gọi I là giao điểm của BM, CN. Gọi E là giao điểm của CN, AP. Gọi F là giao điểm của AP, BM. Khi đó, diện tích của tam giác. Khi đó, ta có:
Bên trong một hình vuông có cạnh bằng 1 cho 1000 điểm trong đó không có ba điểm nào thẳng hàng. Nếu trong số các tam giác có đỉnh là 3 trong 1000 điểm đó thì
Cho ABC vuông cân tại A có BC = 36cm. Vẽ hình chữ nhật MNPQ sao cho . Khi đó, diện tích hình chữ nhật MNPQ là
Cho hình thang cân ABCD (AB // CD). Biết BD = 7 cm; . Tính diện tích hình thang ABCD.
Cho ABC, trên tia đối của các tia BA, CB, AC lấy M, N, P sao cho BM = BA, CN = CB, AP = AC. Kết luận nào sau đây là đúng?
Gọi M, N lần lượt là trung điểm các cạnh BC và CD của tứ giác lồi ABCD.
Khẳng định nào sau đây là đúng?
Cho ABC nội tiếp KMN và KMN nội tiếp PQR trong đó . Biết . Tính .
Tính diện tích hình thang ABCD có cạnh bên AD = a, khoảng cách từ trung điểm E của BC đến AD bằng h.
Cho tứ giác ABCD có diện tích là . Gọi M; N lần lượt là trung điểm AB; CD. Gọi P; Q lần lượt là trung điểm BM và DN. Diện tích tứ giác là
Cho lục giác đều ABCDEF. Gọi M, K lần lượt là trung điểm của CD và DE. Gọi H là giao điểm của AM và BK. So sánh diện tích tam giác ABH và diện tích tứ giác MDKH.
Cho tam giác ABC với D là điểm thuộc cạnh BC và F là điểm thuộc cạnh AB. Điểm K đối xứng với điểm B qua DF. Biết rằng K, B nằm khác phía so với AC. Cạnh AC cắt FK tại P và DK tại Q. Tổng diện tích của các tam giác AFP, PKQ và QDC là . Nếu ta cộng tổng diện tích này với diện tích tứ giác DFPQ thì bằng diện tích tam giác ABC. Diện tích tam giác ABC là
Cho hình bình hành ABCD, đường DP đi qua trung điểm N của BC và cắt đường thẳng AB tại P. Từ đỉnh C vẽ đường thẳng CQ qua trung điểm M của AD và cắt đường thẳng AB tại Q. Đường thẳng DP và CQ cắt nhau tại O. Biết diện tích hình bình hành ABCD là k. Tính diện tích tam giác QPO theo k.
Cách tính diện tích đa giác
• Với một đa giác bất kì không có công thức tính. Cụ thể, ta có thể thực hiện các cách sau để tính diện tích đa giác:
+ Chia đa giác đó thành các tam giác riêng biệt rồi tính diện tích từng tam giác sau đó cộng các kết quả lại với nhau.
+ Tạo ra một tam giác chứa đa giác đó rồi tính diện tích đa giác bằng cách lấy tam giác lớn trừ đi diện tích của các “phần thừa”.
• Với một số hình đặc biệt ta có thể chia đa giác thành nhiều phần, mỗi phần đều là những hình mà ta dễ tính diện tích như: hình thang vuông, hình thoi, hình chữ nhật, hình vuông,...
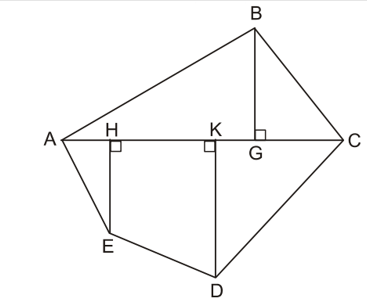
Ví dụ: Để tính diện tích đa giác ABCDE, từ B, D, E lần lượt dựng các đường cao BG, DK, EH (G, K, H Î AC).
Khi đó, diện tích đa giác ABCDE bằng tổng diện tích các hình: tam giác ABC, tam giác CDK, hình thang DEHK và tam giác AEH.